5 . Колебания магнита

Вася Лисичкин , известный на всю школу экспериментатор, решил заставить колебаться магнитную фигурку любимого литературного героя Колобка по стенке холодильника. Он прикрепил фигурку к пружине жесткостью k = 10 H/м, растянул ее на 10 см и отпустил. Сколько колебаний совершит Колобок, если масса фигурки m = 10 г, коэффициент трения между фигуркой и стенкой равен μ = 0,4 , а оторвать ее от стенки можно силой F = 0,5 Н.

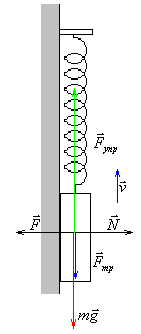
Решение

1. П ри движении из крайнего нижнего в крайнее верхнее положение, когда скорость груза направлена вверх, сила трения скольжения направлена вниз и численно равна . Таким образом, пружинный маятник находится в постоянном силовом поле, созданном силами тяжести и трения. В постоянном силовом поле у маятника смещается положения равновесия:

где - растяжение пружины в новом «положении равновесия»

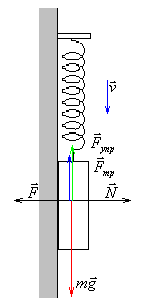2. П ри движении из крайнего верхнего в крайнее нижнее положение, когда скорость груза направлена вниз, сила трения скольжения направлена вверх и численно равна . Таким образом, пружинный маятник опять-таки находится в постоянном силовом поле, созданном силами тяжести и трения. В постоянном силовом поле у маятника смещается положения равновесия:

где - деформация пружины в новом «положении равновесия», знак «-» говорит, что в этом положении пружина сжата.

3. Зона застоя ограничена деформациями пружины от - 1 см до 3 см и составляет 4 см. Середина зоны застоя, в которой деформация пружины равна 1 см, соответствует положению груза, в котором сила трения отсутствует. В зоне застоя сила упругости пружины по модулю меньше равнодействующей максимальной силы трения покоя и силы тяжести. Если маятник останавливается в зоне застоя, колебания прекращаются.

4. За каждый период деформация пружины уменьшается на две ширины зоны застоя, т.е. на 8 см.

После одного колебания деформация пружины станет равной 10 см – 8 см = 2 см. Это означает, что после одного колебания фигурка Колобка попадает в зону застоя и ее колебания прекращаются.

Тест «Затухающие колебания»

1. Под затуханием колебаний понимают…

А. уменьшение частоты колебаний.

Б. уменьшение периода колебаний.

В. уменьшение амплитуды колебаний.

Г. уменьшение фазы колебаний.

2. Причина затухания свободных колебаний –

А. действие на систему случайных факторов, тормозящих колебания.

Б. действие периодически изменяющейся внешней силы.

В. наличие в системе силы трения.

Г. постепенное уменьшение квазиупругой силы, стремящейся вернуть маятник в положение равновесия.

3. Из приведенных ниже уравнений движения выберите то, которое соответствует затухающим колебаниям в системе с вязким трением.

А.

Б.

В.

Г.

4. Два одинаковых математических маятника колеблются, один в вакууме, другой в сжатом воздухе . Сравните период колебания Т маятника в воздухе с периодом колебания маятника в вакууме .

А. Т > Б. Т < В. Т =

5. Математический маятник начал колебаться с амплитудой 9 см. Через некоторое время амплитуда колебаний стала равной 6 см. Какой будет амплитуда колебаний через следующий промежуток времени ?

А. 5 см Б. 4 см В. 3 см

Г. Ответ дать не возможно, поскольку неизвестно время .

6. Два одинаковых маятника, находясь в разных вязких средах, совершают колебания. Амплитуда этих колебаний меняется с течением времени так, как показано на рисунке. В какой среде трение больше?

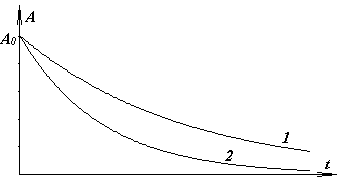
А. 1

Б. 2

В. ответ дать невозможно, поскольку по осям координат не проставлен масштаб и выполнить расчеты нельзя.

7. Два маятника, находясь в одинаковых средах, совершают колебания. Амплитуда этих колебаний меняется с течением времени так, как показано на рисунке. Какой маятник имеет большую массу?

А. 1

Б. 2

В. ответ дать невозможно, поскольку по осям координат не проставлен масштаб и выполнить расчеты нельзя.

8. На каком рисунке правильно показана зависимость координаты затухающих колебаний в системе с вязким трением от времени?

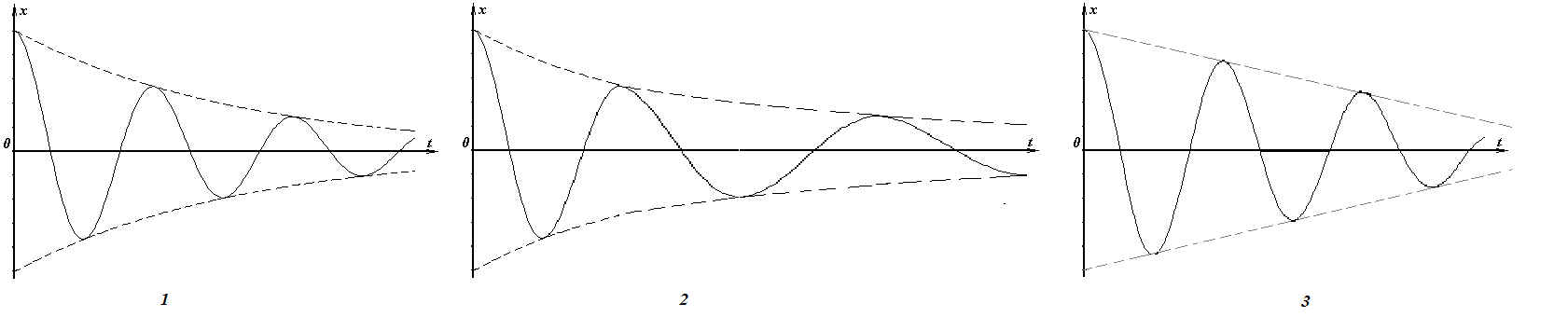
1. 1 Б. 2 B. 3 Г. Все графики верные

9. Установите соответствие между физическими величинами, характеризующими затухание колебаний в системах с вязким трением, и их определением и физическим смыслом. Заполните таблицу

Физическая величина	Определение, физический смысл	расчетная формула
Время релаксации
Декремент затухания
Логарифмический декремент затухания

А. Это отношение амплитуд колебаний через время, равное периоду.

Б. Это натуральный логарифм отношения амплитуд колебаний через время, равное периоду.

В. Это время, в течение которого амплитуда колебаний уменьшается в е раз.

Г.

Д.

Е.

Ж. Эта величина обратна числу колебаний, за которое амплитуда колебаний уменьшается в е раз.

З. Эта величина показывает во сколько раз уменьшается амплитуда колебаний за время, равное периоду колебаний.

10. Составьте правильное утверждение.

Под добротностью понимают…

А. увеличенное в 2p раз отношение полной энергии системы E к энергии W , рассеянной за период;

Б. отношение амплитуд через промежуток времени, равный периоду;

В. количество колебаний, которое совершает система к тому моменту, когда амплитуда уменьшится в е раз.

Добротность рассчитывают по формуле…

А. ;

Б. ;

В. .

Добротность колебательной системы зависит от…

А. энергии системы;

Б. потерь энергии за период;

В. параметров колебательной системы и трения в ней.

Чем больше добротность колебательной системы, тем …

А. медленнее затухают колебания.

Б. быстрее затухают колебания.

11. Математический маятник приводят в колебательное движение, отклонив подвес от положения равновесия в первом случае на 15°, во втором – на 10°. В каком случае маятник совершит больше колебаний до остановки?

А. когда подвес отклонили на 15°;

Б. когда подвес отклонили на 10°;

В. в обоих случаях маятник совершит одинаковое число колебаний.

12. К двум нитям одинаковой длины прикрепили шарики одинакового радиуса – алюминиевый и медный. Маятники приводят в колебательное движение, отклонив их на одинаковые углы. Какой из маятников совершит большее количество колебаний до остановки?

А. алюминиевый;

Б. медный;

В. оба маятника совершат одинаковое количество колебаний.

13. Пружинный маятник, расположенный на горизонтальной поверхности, привели в колебания, растянув пружину на 9 см. После совершения трех полных колебаний маятник оказался на расстоянии 6 см от положения недеформированной пружины. На каком расстоянии от положения недеформированной пружины окажется маятник после следующих трех колебаний?

А. 5 см Б. 4 см В. 3 см

14. Пружинный маятник, состоящий их груза массой m и пружины жесткостью k, совершает колебания на горизонтальном столе. Коэффициент трения между грузом и поверхностью стола равен . Сравните период колебания Т маятника с трением с периодом колебания идеального маятника .

А. Т >

Б. Т <

В. Т =

15. Пружинный маятник совершает колебания на горизонтальной шероховатой поверхности стола. Какой из графиков правильно отражает зависимость координаты маятника от времени?

А. 1 Б. 2 В. 3

Г. Любой из графиков может оказаться верным в зависимости от параметров колебательной системы и величины коэффициента трения

16. Пружинный маятник, состоящий их груза массой m = 200 г и пружины жесткостью k = 20 Н/м, совершает колебания на горизонтальном столе. Коэффициент трения между грузом и поверхностью стола равен . На какую величину изменяется амплитуда колебаний маятника за каждый период?

А. 1 см Б. 2 см В. 3 см Г. 4 см

Задачи для самостоятельного решения

1. Амплитуда затухающих колебаний маятника за время t₁ = 5 мин уменьшилась в n₁ = 2 раза. За какое время t₂ амплитуда уменьшится в n₂ = 8 раз?

2. За время t = 8 мин амплитуда затухающих колебаний уменьшилась в 3 раза. Определите коэффициент затухания d. Какова добротность этой колебательной системы, если период колебаний Т = 10 с. Сколько полных колебаний совершит система до полной остановки?

3. Логарифмический декремент затухания маятника равен q = 3×10^-3. Определите число полных колебаний, которое должен совершить маятник, чтобы амплитуда его колебаний уменьшилась в 2 раза.

4. Определите период Т затухающих колебаний системы, если период собственных колебаний Т = 1 с, а логарифмический декремент затухания равен q = 0, 628.

5. Определите добротность маятника, если за время, в течение которого было совершено 10колебаний, амплитуда уменьшилась в 2 раза. Сколько колебаний совершит маятник до остановки? За какое время это произойдет?

6. Энергия затухающих колебаний маятника за время t = 100 с уменьшилась в 100 раз. Определите коэффициент сопротивления среды r, если масса маятника 100 г.