Вопрос 2. Как быстро затухают колебания в системах с вязким трением?

2.1 Декремент затухания.

Мы показали, что при наличии вязкого трения в системе она совершает колебания,

а мплитуда которых убывает по экспоненциальному закону:

Б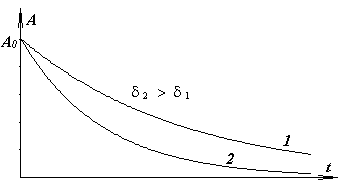 ыстрота затухания (убывания амплитуды) зависит от трения в системе: чем больше коэффициент сопротивления , тем больше значение величины . Видно, что величина  характеризует быстроту затухания колебаний. По этой причине  называют коэффициентом затухания.

Для электрических колебаний в контуре коэффициент затухания зависит от параметров катушки: чем больше активное сопротивление катушки, тем быстрее убывают амплитуды заряда на конденсаторе, напряжения, силы тока.

Ф ункция является произведением убывающей показательной функции и гармонической функции , поэтому функция не является гармонической. Но обладает определенной степенью «повторяемости», заключающейся в том, что максимумы, минимумы, нули функции наступают через равные промежутки времени. График функции представляет собой синусоиду, ограниченную двумя экспонентами.

Н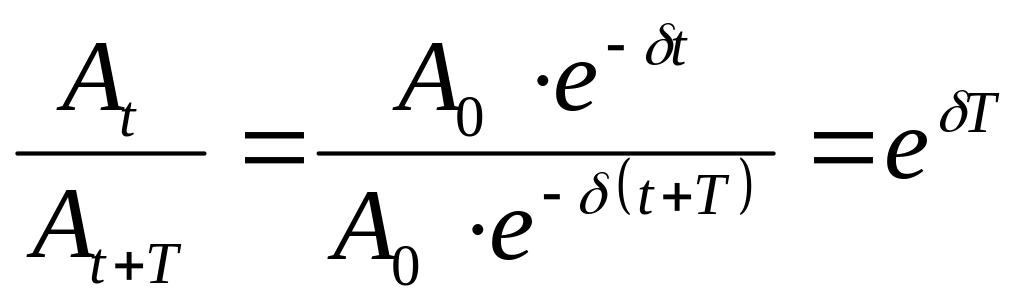 айдем отношение двух последовательных амплитуд, разделенных промежутком времени в один период. Это отношение называют декрементом затухания.

Обратите внимание, что результат не зависит от того, какие два последовательных периода вы рассматриваете – в начале колебательного движения или по прошествии какого-то времени. За каждый период амплитуда колебаний меняется не на одинаковую величину, а в одинаковое количество раз!!

Нетрудно видеть, что за любые разные промежутки времени амплитуда затухающих колебаний уменьшается в одинаковое количество раз.

2.3 Время релаксации.

В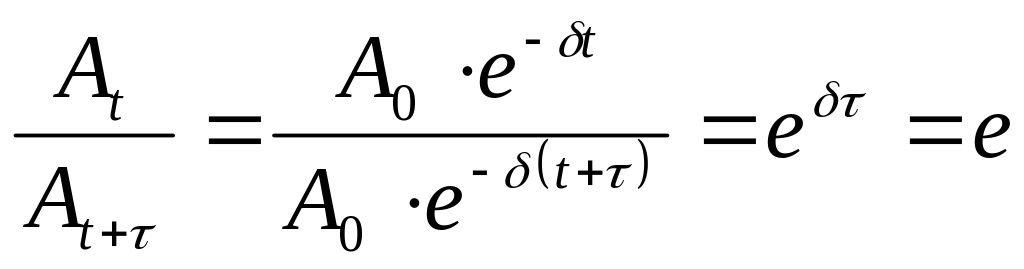 ременем релаксации называется время , за которое амплитуда затухающих колебаний уменьшается в е раз:

Тогда .

О тсюда нетрудно установить физический смысл коэффициента затухания:

Таким образом, коэффициент затухания есть величина, обратная времени релаксации . Пусть, например, в колебательном контуре коэффициент затухания равен . Это значит, что через время с амплитуда колебаний уменьшится в е раз.

2.2 Логарифмический декремент затухания.

Ч асто быстроту затухания колебаний характеризуют логарифмическим декрементом затухания. Для этого берут натуральный логарифм от отношения амплитуд, разделенных промежутком времени в период.

Выясним физический смысл логарифмического декремента затухания.

П усть N – число колебаний, совершаемых системой за время релаксации, то есть число колебаний, за которое амплитуда колебаний уменьшается в е раз. Очевидно, . Тогда

Видно, что логарифмический декремент затухания - есть величина, обратная числу колебаний, по прошествии которых амплитуда уменьшается в е раз.

Допустим, , это значит, что по прошествии 100 колебаний амплитуда уменьшится в е раз.

2.3 Добротность колебательной системы.

Кроме логарифмического декремента затухания и времени релаксации, быстроту затухания колебаний можно характеризовать такой величиной, как добротность колебательной системы. Под добротностью понимают увеличенное в 2 раз отношение полной энергии системы Е к энергии W , рассеянной за период:

Очевидно, что чем меньше энергии рассеивается за период за счет работы силы сопротивления, тем больше добротность колебательной системы. В идеальном случае (при отсутствии потерь) добротность колебательной системы стремится к бесконечности.

М ожно показать, что для слабо затухающих колебаний

***

Энергия колебательной системы в произвольный момент времени равна . Потери энергии за период можно найти как разность энергии в момент времени и энергии через время, равное периоду:

Т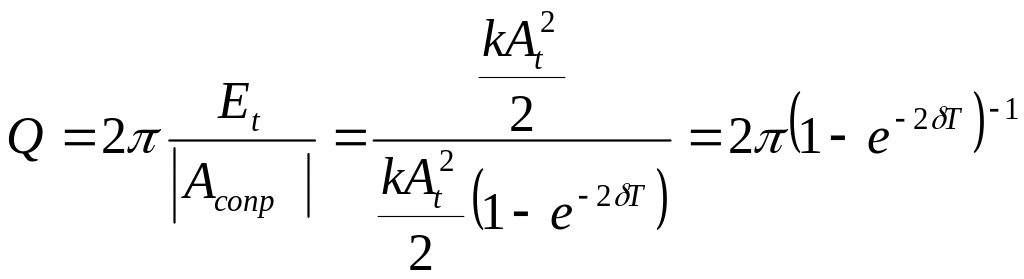 огда

Показательную функцию можно разложить в ряд при << 1. после подстановки получаем .

При выводе нами было наложено ограничение << 1, что верно только для слабо затухающих колебаний. Следовательно, область применения выражения для добротности ограничена только слабо затухающими колебаниями. Тогда как выражение применимо к любой колебательной системе.

Формулы, полученные нами для добротности системы, пока ни о чем не говорят. Допустим, расчеты дают значение добротности Q = 10. Что это означает? Как быстро затухают колебания? Это хорошо или плохо?

Обычно условно считают, что колебания практически прекратились, если их энергия уменьшилась в 100 раз (амплитуда – в 10). Выясним, какое количество колебаний совершила система к этому моменту:

М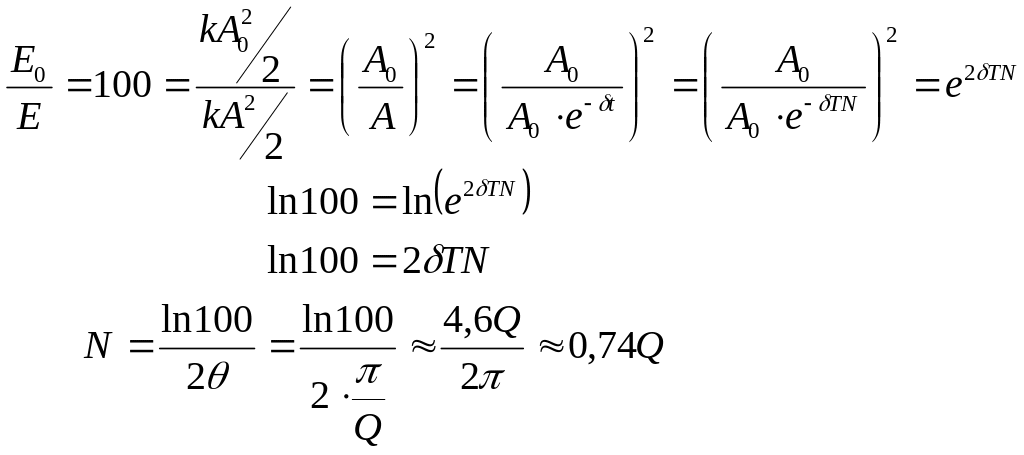 ожем ответить на поставленный ранее вопрос: N = 8.

Какая колебательная система лучше – с большой или малой добротностью? Ответ на этот вопрос зависит от того, что вы хотите получить от колебательной системы.

Если вы желаете, чтобы система совершила как можно больше колебаний до остановки, добротность системы нужно увеличивать. Как? Поскольку добротность определяется параметрами самой колебательной системы, то необходимо правильно эти параметры подобрать.

Н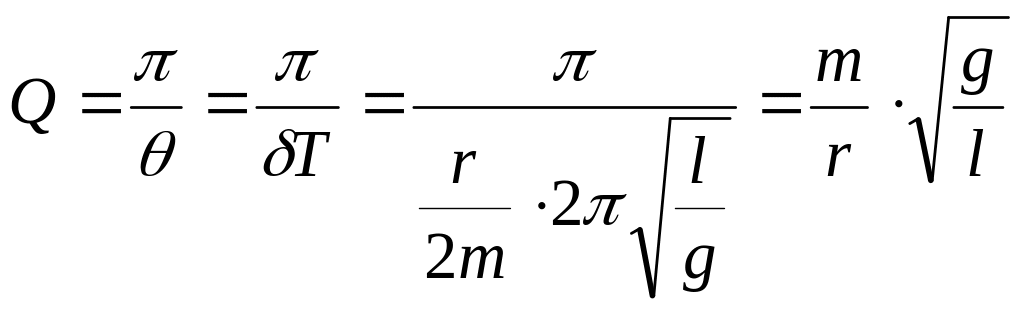 апример, маятник Фуко, установленный в Исаакиевском соборе, должен был совершать слабо затухающие колебания. Тогда

Самый простой способ увеличить добротность маятника – сделать его тяжелее.

В практике нередко возникают и обратные задачи: необходимо по возможности быстрее погасить возникшие колебания (например, колебание стрелки измерительного прибора, колебания кузова автомобиля, колебания судна и т.д.) приспособления, позволяющие увеличить затухание в системе, называются демпферами (или амортизаторами)

Например, амортизатор автомобиля в первом приближении представляет собой цилиндр, заполненный маслом (вязкой жидкостью), в котором может двигаться поршень, имеющий ряд мелких отверстий. Шток поршня соединен с кузовом, а цилиндр – с осью колеса. Возникшие колебания кузова быстро затухают, так как движущийся поршень встречает на своем пути большое сопротивление со стороны вязкой жидкости, заполняющей цилиндр.