22

Лекция 4. Затухающие колебания.

В реальных механических колебательных системах при выведении их из положения равновесия кроме квазиупругой силы действует сила трения. Поскольку она направлена против скорости, работа силы трения отрицательна. Эта работа приводит к уменьшению полной механической энергии колебательной системы

У меньшение энергии колебательной системы приводит к постепенному уменьшению амплитуды колебаний, ибо

В этом случае говорят, что колебания затухают.

Аналогичная ситуация складывается в колебательном контуре. Реальная катушка, входящая в состав контура, всегда обладает активным сопротивлением . При протекании тока на активном сопротивлении катушки будет выделяться джоулево тепло . Энергия контура при этом будет уменьшаться, что будет приводить к уменьшению амплитуды колебаний заряда, напряжения и силы тока.

Наша задача – выяснить по какому закону происходит уменьшение амплитуды колебаний, по какому закону изменяется сама колеблющаяся величина, с какой частотой происходят затухающие колебания, как долго колебания «затухают».

Вопрос 1. Затухание колебаний в системах с вязким трением.

Рассмотрим колебательную систему, в которой действует сила вязкого трения. Примером такой колебательной системы может служить математический маятник, совершающий колебания в воздушной среде.

В этом случае при выведении системы из положения равновесия на маятник будут действовать две силы: квазиупругая сила и сила сопротивления (сила вязкого трения). Второй закон Ньютона запишется следующим образом:

М ы знаем, что при малых скоростях сила вязкого трения пропорциональна скорости движения:

Знак «-» указывает на то, что сила вязкого трения всегда направлена против скорости движения тела.

Т огда выражение (1) в проекции на ось ОХ, вдоль которой происходят колебания, будет выглядеть следующим образом:

У чтем, что проекция скорости есть первая производная от координаты тела, а проекция ускорения – вторая производная от координаты:

Т огда уравнение (2) примет вид:

Р азделив все члены уравнения на m и обозначив

п олучим уравнение движения в следующем виде:

 - коэффициент затухания, он зависит от коэффициента трения r,

₀ - циклическая частота идеальных колебаний (в отсутствие трения).

П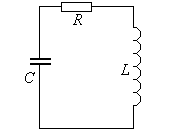 режде чем решать уравнение (3), рассмотрим колебательный контур. Активное сопротивление катушки включено последовательно с емкостью С и индуктивностью L.

З апишем второй закон Кирхгофа

Учтем, что

, , .

Т огда второй закон Кирхгофа примет вид:

Р азделим обе части уравнения на :

В ведем обозначения

Окончательно получаем

Обратите внимание на математическую тождественность дифференциальных уравнений (3) и (3’). В этом нет ничего удивительного. Мы уже показывали абсолютную математическую тождественность процесса колебания маятника и электромагнитных колебаний в контуре. Очевидно, процессы затухания колебаний в контуре и в системах с вязким трением происходят тоже одинаково.

Решив уравнение (3), мы получим ответы на все поставленные выше вопросы.

У равнение (3) можно привести к уравнению гармонических колебаний, применив подстановку

Т огда уравнение (3) примет вид

Е сли ²  ₀², то величина ₀² - ²  0, ее можно обозначить ² = ₀² - ² . Получаем знакомое уравнение гармонических колебаний.

Решение этого уравнения нам известно

Тогда для искомого уравнения (3) получаем окончательный результат

Нетрудно видеть, что заряд конденсатора в реальном колебательном контуре будет изменяться по закону

Анализ полученного результата:

1. В результате совместного действия квазиупругой силы и силы сопротивления система может совершать колебательное движение. Для этого должно выполняться условие ₀² - ²  0. Иными словами, трение в системе должно быть невелико.

2. Частота затухающих колебаний  не совпадает с частотой колебаний системы в отсутствие трения ² = ₀² - ²  ₀². С течение времени частота затухающих колебаний остается неизменной.

3. Если коэффициент затухания  мал, то частота затухающих колебаний близка к собственной частоте ₀ . При ²  ₀² частота уменьшается, а период возрастает до бесконечности. При ² ₀² колебаний не возникает: система, выведенная из положения равновесия, медленно (апериодически) возвращается в положение равновесия.

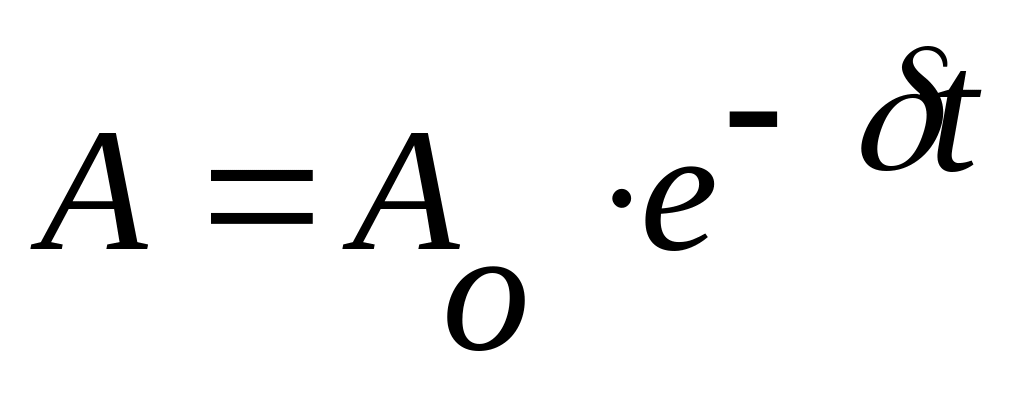4. А мплитуда затухающих колебаний, как это и было предсказано ранее, уменьшается с течением времени.

Это убывание амплитуды происходит по экспоненциальному закону.

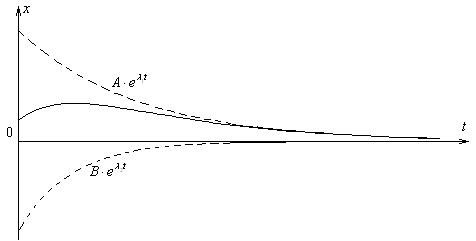
5. Если ₀² - ² < 0, то есть трение в системе велико, то уравнение (3) имеет решение вида

где . Непосредственной подстановкой легко убедиться, что функция (4) действительно является решением уравнения (3). Очевидно, что сумма двух экспоненциальных функций не является периодической функцией. С физической точки зрения это означает, что колебания в системе не возникнут. После выведения системы из положения равновесия она будет медленно в него возвращаться. Такой процесс называется апериодическим.

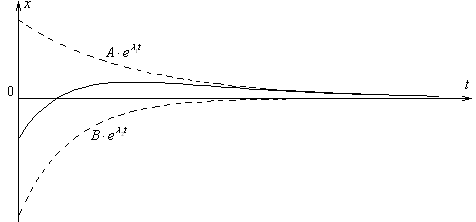и ли