2. Принцип максимума Понтрягина и решение задачи о быстродействии при переводе материальной точки в начало координат.
В
рамках вариационных методов задача
синтеза оптимального управления
решается без огра-ничений на характер
управления. На практике управление
часто имеет существенные ограни-чения
в форме замкнутых допустимых подмно-жеств
своих значений. Использование методов
вариационного исчисления при наличии
по-добных ограничений на управление
невозможно. Необходимые условия
оптималь-ности управления в
таких задачах
дает принцип максимума Понтрягина.
Рассмотрим
классическую задачу Больца
,
где моменты времени
,
T
считаем заданными, как и начальное
значение
.
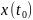Задача Больца всегда может быть сведена
к задаче Майера. Для этого вводится
новая переменная
,
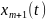и
новый
расширенный вектор состояний
.
,
.
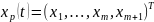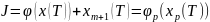
Вводится
дополнительное ограничение на управление
.
Если множество
замкнуто и ограничено, то оптимальное
управление может принадлежать границе
множества. В этом случае варьировать
управление произвольным образом
нельзя.В
рамках принципа максимума Понтрягина
доказывается следующая теорема.
Пусть
– оптимальное управление, а
– оптимальная траектория. Тогда
существует вектор
,
удовлетворяющий уравнениям
,
такой,
что функция
имеет
максимум
Максимум
функции вычисляется по параметрам
управления u
при фиксированных
значениях остальных параметров. Если
ввести
то
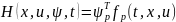в задаче Майера. Таким образом, построение
оптимального управления производится
последующей схеме:
управление сначала определяется на основе максимизации гамильтониана как функция
;
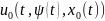затем найденное управление подставляют
в уравнение для
и
и решают полученную краевую задачу
относительно
;
подставляют найденные
в выражение для
,
получая при этом явный вид
.
Подобное
решение задачи управления является
оптимальным, если решение исходной
задачи существует, а решение краевой
задачи единственно. По сравнению с
необходимыми условиями оптимальности
в классической вариационной задаче в
принципе максимума заменено только
условие стационарности
на условие максимума. Рассмотрим
использование данного метода в задаче
управления, если определена не только
начальная
,
но и конечная точка
,
но не определено время T
и требуется минимизировать функционал
,
.
Такая
задача называется задачей о быстродействии.
Задача о быстродействии также может быть сведена к задаче Майера. Введем вектор
,
.
Тогда
задача поиска оптимального управления
сводится к задаче минимизации функционала
,
то есть по форме к задаче Майера.
Гамильтониан в данной задаче имеет вид
(если ввести
)
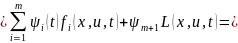
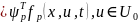.Рассмотрим
в качестве конкретного примера
задачу о минимизации времени перевода
материальной точки, движущейся по
прямой с начальной скоростью
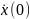из заданного начального состояния
x(0),
в начало координат с нулевой конечной
скоростью (задача
об управлении лифтом).
Пусть
– координата, а
– скорость. Тогда уравнение движения
и краевые условия к нему имеют вид
,
.
Управление u(t)
в данном случае определяет ускорение,
для которого нужно ввести ограничения.
Пусть
.Выбором
управления требуется перевести систему
в начало координат за минимальное время
.
В данном случае гамильтониан имеет вид
.
Система сопряженных уравнений имеет
вид
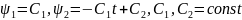.Максимум
функции H
обеспечивается для ограничения
при условии
,
Пусть
на некотором интервале времени
.
Тогда движение системы происходит по
параболам
,
.
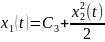Если же в течение некоторого интервала
времени
то
.
Так как функция
,
то оптимальное управление может иметь
только одну точку переключения (изменения
знака) и два интервала постоянства
уровней.
Контрольно-измерительный материал № 19