
- •Определение систем в рамках теоретико - множественного подхода. Математические модели простых динамических систем.
- •Принцип разделения в цифровых системах управления. Обоснование для линейно – квадратичной задачи управления в дискретном времени.
- •Решение задачи линейного программиро-вания на основе симплекс- метода.
- •Общая постановка задачи оптимальной фильтрации и методика ее решения.
- •Кибернетический подход к описанию систем. Понятия об управлении, системе управления, структурные схемы процесса управления.
- •Теорема о нормальной корреляции и ее следствия.
- •Классификация систем управления. Основ-ные этапы синтеза сложных систем управления.
- •Метод анализа иерархий.
- •Устойчивость динамических систем. Теорема Ляпунова в непрерывном и дискретном времени.
- •Иерархическая схема управления сложным объектом. Основные принципы иерархического управления.
- •Управляемость и наблюдаемость систем управления.
- •Решение задачи о пошаговом распределении ресурсов (динамического программирования) на основе принципа оптимальности Беллмана.
- •Постановка и пример задачи автоматичес-кого управления для непрерывных динамичес-ких систем. Задачи Больца, Лагранжа, Майера.
- •Метод анализа иерархий.
- •Общее решение задачи автоматического управления без ограничений для детерминиро-ванной системы на основе методов вариации-онного исчисления.
- •Цифровая схема управления (общая схема преобразований). Эквивалентность цифровой и непрерывной систем.
- •Решение линейно – квадратичной задачи нахождения оптимального управления для динамической системы в непрерывном времени на основе методов вариационного исчисления.
- •Управление ресурсами и задача линейного программирования. Примеры, геометрическая интерпретация.
- •Решение задачи линейного программиро-вания на основе симплекс – метода.
- •Теорема о нормальной корреляции и ее следствия.
- •Решение задачи линейного программиро-вания на основе симплекс – метода
- •2.Общая постановка задачи оптимальной фильтрации и методика ее решения.
- •Линейный регулятор. Пример решения задачи лк – управления.
- •2. Синтез структуры сложной системы управления. Метод ветвей и границ.
- •Принципы координации в задачах управления сложными объектами.
- •2. Решение задачи о пошаговом распределении ресурсов (динамического программирования) на основе принципа оптимальности Беллмана.
- •Кибернетический подход к описанию систем. Понятия об управлении, системе управления, структурные схемы процесса управления.
- •Решение линейно – квадратичной задачи нахождения оптимального управления для динамической системы в непрерывном времени на основе методов вариационного исчисления.
- •Метод анализа иерархий.
- •2. Цифровая схема управления (общая схема преобразований). Эквивалентность цифровой и непрерывной систем.
- •Общее решение задачи автоматического управления без ограничений для детерминированной системы на основе методов вариационного исчисления.
- •2. Оптимальное управление в стохастических системах. Принцип разделения в непрерывных стохастических системах.
- •Принципы координации в задачах управления сложными объектами.
- •2. Уравнения фильтра Калмана в дискретном времени. Пример постановки задачи стохастического управления (управление нефтехранилищем).
- •Синтез структуры сложной системы управления. Метод ветвей и границ.
- •2. Принцип максимума Понтрягина и решение задачи о быстродействии при переводе материальной точки в начало координат.
- •Линейный регулятор. Пример решения задачи лк – управления.
- •2. Решение задачи о пошаговом распределении ресурсов на основе принципа оптимальности Беллмана.
- •Принцип максимума Понтрягина и решение задачи о быстродействии (задача о «лифте»).
- •2. Применение микропроцессоров и микро – эвм в цифровых системах управления.
Цифровая схема управления (общая схема преобразований). Эквивалентность цифровой и непрерывной систем.
Главное достоинство цифровых систем управления состоит в возможности реализации любых, сколь угодно сложных, алгоритмов управления, а также адаптации и коррекции управления с учетом изменения внешних условий. Математические модели поведения простых объектов управления в цифровых системах описываются в дискретном времени на основе разностных линейных и нелинейных уравнений.
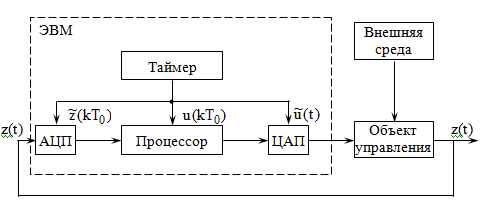
Система включает две основные части: объект управления и управляющую ЭВМ одного из перечисленных выше классов. В состав ЭВМ входят:
АЦП
– аналогово-цифровой преобразователь
непрерывных сигналов наблюдения за
состоянием объекта в дискретную во
времени последователь-ность чисел
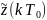 ,
где
,
где
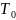 – период формирования последовательности
(интервал дискретизации); ЦАП –
цифро-аналоговый преобразователь
дискретной во времени последовательности
выходных команд управления
– период формирования последовательности
(интервал дискретизации); ЦАП –
цифро-аналоговый преобразователь
дискретной во времени последовательности
выходных команд управления
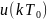 в непре-рывный во времени сигнал
управления
в непре-рывный во времени сигнал
управления
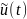 ;
;
процессор, реализующий выполнение управляя-ющей программы с учетом текущих данных наблюдения за состоянием объекта управления и априорных данных о модели его поведения;
таймер синхронизации работы системы в реальном времени.
ЭВМ
функционирует последовательно в режиме
разделения времени и обслуживает
отдельные каналы управления различными
объектами. Каждый из этих каналов имеет
в общем случае свою периодичность
дискретизации процессов
 и свою временную диаграмму обслуживания
различных объектов управления. Процесс
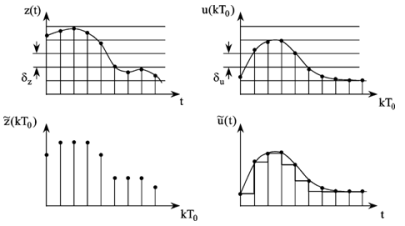
преобразования сигналов в АЦП и в ЦАП
сопровождается их квантованием
по уровню
– в замене мгновенного значения
непрерывнозначной величины (уровня
сигнала) ближайшим разрешенным дискретным
значением. При равномерном
квантовании
в АЦП возникают ошибки, определяемые
соотношением
и свою временную диаграмму обслуживания
различных объектов управления. Процесс
преобразования сигналов в АЦП и в ЦАП
сопровождается их квантованием
по уровню
– в замене мгновенного значения
непрерывнозначной величины (уровня
сигнала) ближайшим разрешенным дискретным
значением. При равномерном
квантовании
в АЦП возникают ошибки, определяемые
соотношением
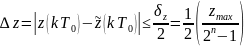 ,
n–
разрядность представления данных в
АЦП;
,
n–
разрядность представления данных в
АЦП;
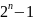 – число уровней квантования;
– число уровней квантования;
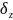 – расстояние между ближайшими уровнями
– цена разряда;
– расстояние между ближайшими уровнями
– цена разряда;
 – диапазон значений амплитуды входного
сигнала
– диапазон значений амплитуды входного
сигнала
 .При
.При
 .При
выполнении обратного преобразования
в ЦАП ошибка определяется следующим
образом:
.При
выполнении обратного преобразования
в ЦАП ошибка определяется следующим
образом:
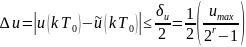 ,
r
– разрядность представления данных
управления на выходе ЦАП;
,
r
– разрядность представления данных
управления на выходе ЦАП;
 – максимальный уровень выходного
сигнала, определяющий диапазон возможных
значений
– максимальный уровень выходного
сигнала, определяющий диапазон возможных
значений
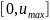 .
Таким
образом,
главная особенность системы управления
с ЭВМ состоит в том, что процесс наблюдения
осуществляется в дискретные моменты
времени с дополнительной погрешностью
канала наблюдения, вносимой шумом
(ошибкой) квантования, которой при
большой разрядности АЦП можно пренебречь.
Условия
эквивалентности непрерывных (аналоговых)
и дискретных (цифровых) систем управления.
Пусть имеется непрерывная детерминированная
система, описываемая уравнениями
.
Таким
образом,
главная особенность системы управления
с ЭВМ состоит в том, что процесс наблюдения
осуществляется в дискретные моменты
времени с дополнительной погрешностью
канала наблюдения, вносимой шумом
(ошибкой) квантования, которой при
большой разрядности АЦП можно пренебречь.
Условия
эквивалентности непрерывных (аналоговых)
и дискретных (цифровых) систем управления.
Пусть имеется непрерывная детерминированная
система, описываемая уравнениями
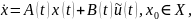
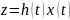 Предположим,
что изменение матриц A(t),
B(t),
h(t)
во времени имеет существенно
медленный по
сравнению с интервалом дискретизации
характер
Предположим,
что изменение матриц A(t),
B(t),
h(t)
во времени имеет существенно
медленный по
сравнению с интервалом дискретизации
характер
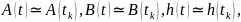
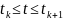 .
В цифровой системе исходный управляющий
сигнал имеет дискретный во времени
характер
.
В цифровой системе исходный управляющий
сигнал имеет дискретный во времени
характер
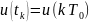 .
Соответственно на выходе ЦАП формируется
непрерывный по времени сигнал ступенчатого
вида. Тогда для фиксированного в момент
.
Соответственно на выходе ЦАП формируется
непрерывный по времени сигнал ступенчатого
вида. Тогда для фиксированного в момент
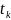 начального состояния x(
)
объекта управления текущее состояние
в интервале между
и
начального состояния x(
)
объекта управления текущее состояние
в интервале между
и
 можно получить как решение дифференциального
уравнения в виде
можно получить как решение дифференциального
уравнения в виде
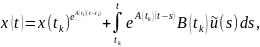
Где
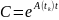 – фундаментальная матрица решения
соответствующего однородного уравнения.
С учетом того, что
– фундаментальная матрица решения
соответствующего однородного уравнения.
С учетом того, что
 не изменяется на интервале
не изменяется на интервале
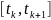 и, проводя замену
и, проводя замену
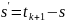 ,
получим
,
получим
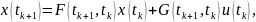
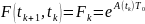 ,
,
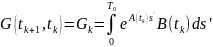
Если
работа АЦП и ЦАП синхронизирована во
времени с помощью таймера, а время
преобразования в них незначительно
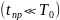 то можно считать, что процессы
то можно считать, что процессы
 и z
дискретизируются в одни и те же моменты
времени.
В
результате вместо непрерывной получаем
эквивалентную дискретную систему
описываемую стандартными уравнениями
и z
дискретизируются в одни и те же моменты
времени.
В
результате вместо непрерывной получаем
эквивалентную дискретную систему
описываемую стандартными уравнениями
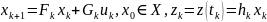 ,
,
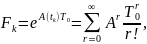
 ;
;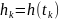 .
Полученное
разностное уравнение является точным
для моментов дискретизации процессов
во времени, так как оно дает при этом
точные значения переменных, описывающих
состояния и наблюдения. При выполнении
указанных технических условий
(синхронизации) для существования
эквивалентной цифровой системы
управления требуется, чтобы существовала
невырожденная матрица
.
Полученное
разностное уравнение является точным
для моментов дискретизации процессов
во времени, так как оно дает при этом
точные значения переменных, описывающих
состояния и наблюдения. При выполнении
указанных технических условий
(синхронизации) для существования
эквивалентной цифровой системы
управления требуется, чтобы существовала
невырожденная матрица

которая
не имела бы отрицательных собственных
чисел. В противном случае логарифм
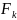 не существует и нельзя получить
взаимно-однозначные отображения
непрерывной и дискретной системы.
Одновременно эти же условия гарантируют
единственность решения для матрицы
не существует и нельзя получить
взаимно-однозначные отображения
непрерывной и дискретной системы.
Одновременно эти же условия гарантируют
единственность решения для матрицы
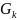 .
.
 .
Аналогичным
образом определяется возможность
построения эквивалентной цифровой
линейной системы при наличии возмущений
состояния и шумов наблюдения. При
малых интервалах дискретизации
цифровая система управления может быть
получена из аналоговой путем замены
функциональных преобразований,
описывающих формирование управления
u(t)
как сигнала в непрерывном времени, их
дискретными эквивалентами. Так, для
линейного ПИД-регулятора, реализующего
преобразования наиболее общего вида,
может быть получен его цифровой
эквивалент следующим образом. уравнение
ПИД-регулятора имеет вид
.
Аналогичным
образом определяется возможность
построения эквивалентной цифровой
линейной системы при наличии возмущений
состояния и шумов наблюдения. При
малых интервалах дискретизации
цифровая система управления может быть
получена из аналоговой путем замены
функциональных преобразований,
описывающих формирование управления
u(t)
как сигнала в непрерывном времени, их
дискретными эквивалентами. Так, для
линейного ПИД-регулятора, реализующего
преобразования наиболее общего вида,
может быть получен его цифровой
эквивалент следующим образом. уравнение
ПИД-регулятора имеет вид
 ,
где e(t)
– сигнал ошибки рассогласования.
Заменяя производную первой разностью,
а интеграл по методу прямоугольников
– суммой, получим
,
где e(t)
– сигнал ошибки рассогласования.
Заменяя производную первой разностью,
а интеграл по методу прямоугольников
– суммой, получим
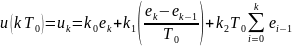 ,
,
 .
.
Контрольно-измерительный материал № 9
