Приложение 2 Расчёт роторов центрифуг на прочность.

1. Предварительные сведения о комплексном (безмоментном и моментном) расчете тонкостенных осесимметричных оболочек вращения.

Из упомянутого раздела курса МХП известно, что ротор центрифуги или сепаратора представляет собой сборочную единицу, сочетающую в себе комбинацию цилиндрической оболочки с конической оболочкой, а также с днищами и крышками плоской, конической или фасонной геометрии. Соединения между этими составными элементами, как правило, являются неразъемными, но в ряде случаев могут быть спроектированы в виде плотно – прочных разъемных соединений. Особенностью расчета роторов является то, что каждый отдельный элемент этой сборочной единицы необходимо рассчитать во взаимосвязи с другими элементами ротора.

Напомним вкратце методику и последовательность расчета статических тонкостенных осесимметричных оболочек вращения, применяемых в оболочечных конструкциях химического оборудования (корпуса технологической аппаратуры, емкости под избыточным давлением).

Это позволит убедиться в аналогии методов прочностного расчета роторов центрифуг и статически установленных осесимметричных тонкостенных оболочек вращения.

Общим свойством оболочек вращения, образующих рабочее пространство ротора, является их осесимметричная форма, геометрия которой рассматривалась в курсе Сопромата и в курсе КРЭОО.

Из этих курсов известно (для случая тонкостенных осесимметричных оболочек), что эти оболочки имеют две группы характерных зон (см. курс КРЭОО.)

Первая группа зон – гладкие участки тонкостенных оболочек без резкого изменения геометрии, жесткости, нагрузки, температурного поля, резкого изменения других существенных физико-механических параметров конструктивного материала оболочек.

Вторая группа зон – так называемые краевые зоны, в которых имеет место резкое изменение отдельных или нескольких вышеперечисленных характеристик и которые распложены в непосредственной близости к местам соединения стыка цилиндрических, конических плоских и фасонных осесимметричных элементов роторов.

В предшествующих курсах рассматривался вопрос расчета статически установленных осесимметричных изотропных оболочек вращения. При этом рассматривалось равновесие бесконечно малого элемента, выделенного из оболочки двумя смежными меридиональными и двумя смежными вторыми главными сечениями. Внешним силовым фактором было внутреннее газовое давление . Внутренними силовыми факторами, определявшими моментное напряженное состояние выделенного элемента были следующие параметры, отнесенные к единице длины дуги срединной поверхности в той грани, где действовал соответствующий внутренний силовой фактор:

- меридиональное нормальное усилие ;

- кольцевое нормальное усилие ;

- меридиональный изгибающий момент ;

- кольцевой изгибающий момент ;

- поперечная сила ;

- краевая сила ;

- краевой изгибающий момент ;

- распорная сила .

В частности и

где и - соответственно меридиональные и кольцевые (тангенциальные) напряжения; - номинальная расчетная толщина стенки оболочки.

Все вышеперечисленные внутренние силовые факторы в приведенной совокупности определяют моментное напряженное состояние. Известно так- же, что вне краевых зон в гладких участках оболочек имеет место лишь безразмерное напряженное состояние, для которого решающими внутренними силовыми факторами являются лишь нормальные силы и . Для безмоментного напряженного состояния основными расчетными соотношениями являются соответственно уравнение Лапласа и уравнение равновесия отсеченной конечной зоны оболочки, т.е.

А) ; Б) .

В реальных инженерных оболочечных конструкциях химического оборудования в узлах сопряжения с другими оболочками, а также с фланцами, трубными решетками и т.п., возникают дополнительные осесимметричные краевые нагрузки, вызывающие локальные нагружения изгиба в кромках сопрягаемых оболочек и деталей. При этом надо отметить то действие краевых и практически полностью затухает на расстоянии 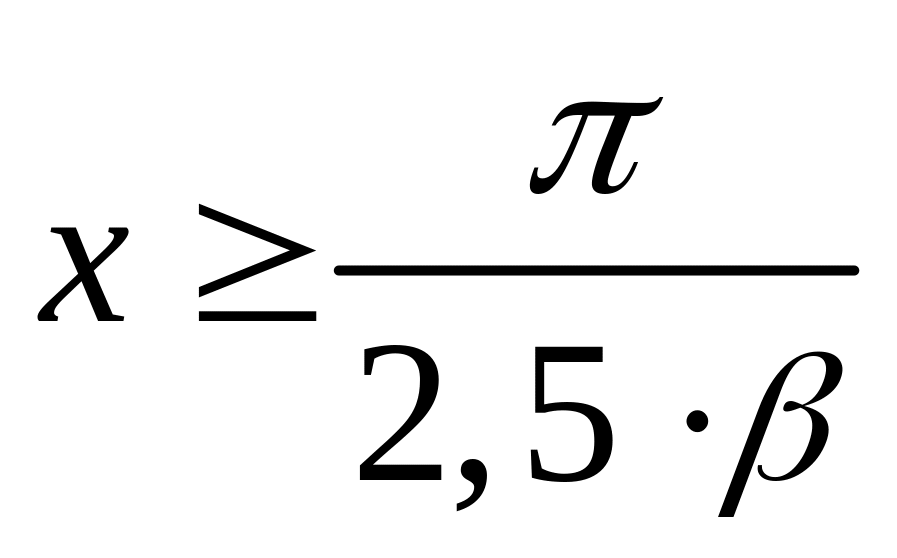от края стыкуемых оболочек ( - коэффициент затухания краевых деформаций вдоль образующей оболочки, определяется по формулам моментной теории оболочек).

Определение краевой силы , действующей в радиальном направлении, и краевого момента , действующего в меридиональном сечении, основано на предположении, что в нормальном работающем узле спряжения оболочек не должно быть каких бы то ни было взаимных перемещений сопрягаемых элементов. Это означает, что алгебраические суммы радиальных и угловых деформаций края одной детали от действующих на него внутренних нагрузок ( и ) и краевых нагрузок ( и ) равны алгебраическим суммам радиальных и угловых деформаций края другой детали от действующих на него соответствующих внутренних и краевых нагрузок (принцип совместности деформаций).

Для иллюстрации приведенного принципа расчета краевых нагрузок рассмотрим простейший пример – узел сопряжения цилиндрической и сферической оболочек (рис.1 ) нагруженных внутренним газовым давлением . На рис.1 а) показана заданная система оболочек, которая с точки зрения

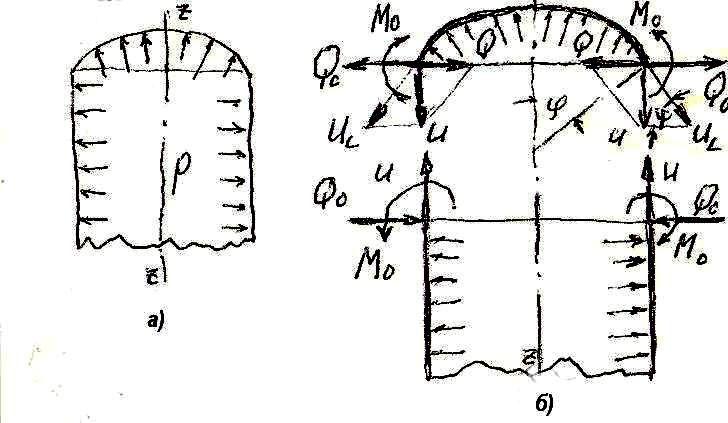
Схема к определению краевых сил и моментов :

а - узел соединения сферической и цилиндрической оболочек;

б – расчетная схема; и - краевые нагрузки; и - меридиональные усилия соответственно цилиндрической и сферической оболочек;

- распорная сила.

Рис 1.

отыскания и является статически неопределимой. Мысленно стык между оболочками рассечен плоскостью, перпендикулярной оси вращения zz. В результате (рис.1 б) получена основная система (статически определимая), которая является гипотетической и состоит из двух оболочек, стыкуемые кромки которых имели бы возможность деформироваться свободно независимо друг от друга под влиянием приложенных внешних нагрузок (внутреннего газового давления , распорной силы , действующей на край сферической оболочки) и определяемых неизвестных краевых нагрузок и . Для определения и составляются недостающие уравнения совместности радиальных и угловых деформаций. Предварительно принимается правило знаков: радиальные перемещения края оболочки в направлении от ее оси положительны; угловые перемещения в направлении по часовой стрелке положительны.

С учетом правила знаков для правой части оболочек запишем уравнения совместности радиальных и угловых деформаций:

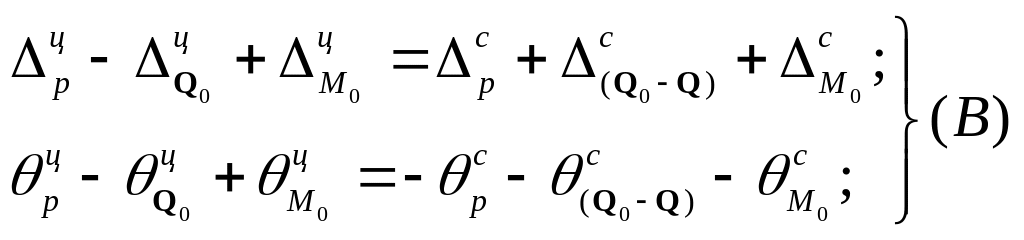
где - соответственно радиальные и угловые деформации края цилиндрической обечайки под действием нагрузок ;

- соответственно радиальные и угловые деформации сферической оболочки под действием нагрузок и .

Необходимо отметить, что записанная система уравнений совместности деформаций (В) применима для так называемых «длинных» оболочек (с позиций оценки протяженности краевой зоны). «Длинными» оболочками считают оболочки, у которых один край удален от противоположного края на расстояние, превышающее протяженность прилегающих краевых зон. При «короткой» оболочке зона действия и распространяется на другой ее край. В этом случае необходимо решать совместно четыре уравнения и определять все неизвестные и .

В дальнейшем, при рассмотрении вопросов прочностного расчета роторов в основном будут рассматриваться «длинные» оболочки.

В расчетной практике в случае роторов центрифуг «длинной» считают такую оболочку, которая удовлетворяет следующим условиям - для цилиндрической - и конической - оболочек соответственно:

,

где - длина ротора, -расстояние от края оболочки до рассматриваемой точки вдоль образующей, - внутренний радиус цилиндрической или максимальный конической оболочки на ее краю, - толщина стенки оболочки, - комплексная величина, зависящая от длины, - коэффициент Пуассона, - угол наклона образующей конуса к его оси.

Следует также отметить, что в случае стыковки в конструкции ротора цилиндрической обечайки с конической или сферической оболочкой в месте стыка (т.е. в краевой зоне) возникает распорная сила , которая, как и другие краевые нагрузки, вызывает соответствующие краевые напряжения. Величина распорной силы, равна проекции меридиональных сил на плоскость, проходящую через стыковое сечение между упомянутыми оболочками и перпендикулярную оси .

При решении краевой задачи в практике проектирования статических оболочек выражения для радиальных и угловых деформаций края стыкуемых оболочек, а так же усилий и , моментов и берут из справочных таблиц, содержащих расчетные формулы моментной и безмоментной теории тонкостенных оболочек.

Таким образом, решив систему уравнений совместности деформации (В) и определив краевые нагрузки и , можно определить суммарные напряжения на наружной и внутренней поверхностях края оболочки:

меридиональные

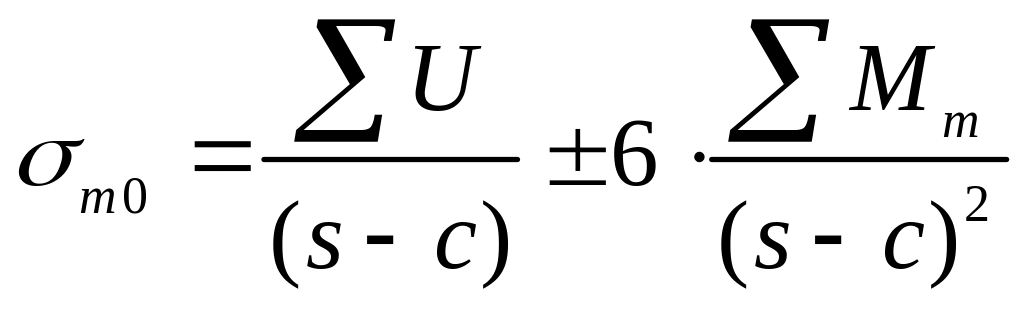или ;

кольцевые

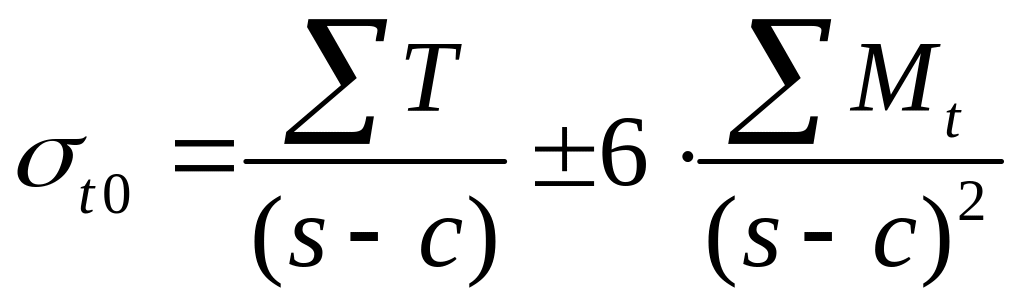или .

Максимальное ,

где , - соответственно сумма меридиональных и сумма тангенциальных (кольцевых) нормальных сил, возникающих на краю обечайки от действия газового давления , краевой и распорной сил, краевых моментов ; , - соответственно сумма меридиональных и сумма тангенциальных (кольцевых) моментов, возникающих на краю обечайки от действия нагрузок и ; - меридиональные напряжения, возникающие на краю обечайки от действия соответственно нагрузок и , - тангенциальные (кольцевые) напряжения, возникающие на краях обечайки от действия соответственно нагрузок и .

На завершающем этапе расчета формируется условие прочности, при этом оценивается величина допускаемого напряжения для краевой зоны .

На основании экспериментальных и теоретических исследований установлено, что при использовании для изготовления пластичных конструкционных материалов при наличии статической нагрузки в рассматриваемых оболочках и в случае преобладания напряжений изгиба допускается увеличение допускаемого напряжения для краевых зон на 30% по сравнению с обычным допускаемым напряжением, т.е. .

Это обстоятельство обосновывается сугубо местным характером зоны влияния краевых напряжений, в которой образуется пластический шарнир, препятствующий разрушению узла стыковки оболочек различной геометрии.

Тогда условие прочности: .

В случае применения для оболочек хрупких конструкционных материалов или конструкционных материалов, покрытых хрупкими покрытиями, а также в случае возникновения в узле сопряжения стыкуемых оболочек циклических нагружений, вышеописанное увеличение допускаемого напряжения для краевых зон не рекомендуется, т.е. для этих случаев должно соблюдаться условие .

Таким образом, освежив в памяти основные этапы и методы расчета статических тонкостенных осесимметричных оболочек вращения, с учетом изученных в настоящем разделе курса МХП мембранных нагрузок во вращающихся роторах центрифуг, можно перейти к алгоритму прочностного расчета таких роторов и к иллюстрации этого алгоритма числовыми примерами.