
- •1 Параметры и связи параметров движения мт
- •3 Криволинейное дв-е мт и его параметры.
- •4 Законы Ньютона для мт
- •5 Эквивалентность работы и энергии при дв-и мт
- •6 Законы взаимодействия мт(сохр-я) в завис-ти от типа взаим-я
- •7 Энергия мт в поле центральных сил
- •8 Силы, проявляющиеся при взаимодействии тел в природе
- •9 Колебательное движение материальной точки
- •10 Понятие центра массы тела и методика определения
- •11,Момент инерции тел, пример его определения. Теорема Штейнера
- •12 Методика сложения сил, прилож-х к разл-м точкам тела и определения их вклада в изменение состояния дв-я
- •13.Параметры и основные законы вращательного движения тел
- •14 Полная механическая энергия тел, степени свободы тел
- •15. Условия статического состояния тел, виды статического состояния
- •16,Колебательное движение твёрдого тела.
- •17 Физическая модель идеального газа, микро и макро параметры
- •18.Мкт.Внутр энергия идеального газа
- •19 Распределение частиц идеального газа по скоростям
- •20.Законы — начала термодинамики
- •21,Работа газа и его теплоёмкость в изопроцессах
- •22,Закон сохранения энергии в изо- и адиабатном процессах.
- •23.Термодинамический цикл. Цикл Карно.
- •24,Теплопроводность газа
- •25 Внутреннее трение в газе
- •26,Диффузия в газе
- •27.Газ в поле тяготения. Барометрическая формула и распределение Больцмана
- •28.Уравнение политропического процесса, уравнение Пуассона
- •29.Термодинамическое определение энтропии
9 Колебательное движение материальной точки
Г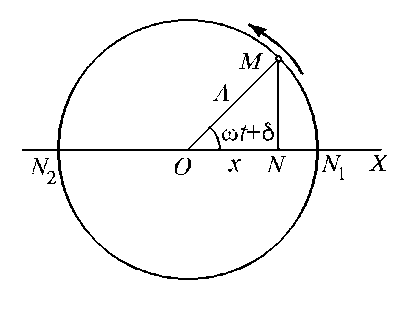 армоническое
колебание.
армоническое
колебание.
Х арактер
такого движения лучше всего раскрывается
с помощью следующей кинематической
модели. Допустим, что геометрическая
точка
арактер
такого движения лучше всего раскрывается
с помощью следующей кинематической
модели. Допустим, что геометрическая
точка
 равномерно вращается по окружности
радиуса
равномерно вращается по окружности
радиуса
 с постоянной угловой скоростью
с постоянной угловой скоростью
 .
Ее проекция
.
Ее проекция
 на диаметр, например на ось
на диаметр, например на ось
 ,
будет совершать колебательное движение
от крайнего положения
,
будет совершать колебательное движение
от крайнего положения
 до другого крайнего положения
до другого крайнего положения
 и обратно. Такое движение точки
называют простым, или гармоническим,
колебанием.
и обратно. Такое движение точки
называют простым, или гармоническим,
колебанием.

Гармоническое колебание груза на пружине.

Все изложенное здесь может быть применено к гармоническим колебаниям любых механических систем с одной степенью свободы.
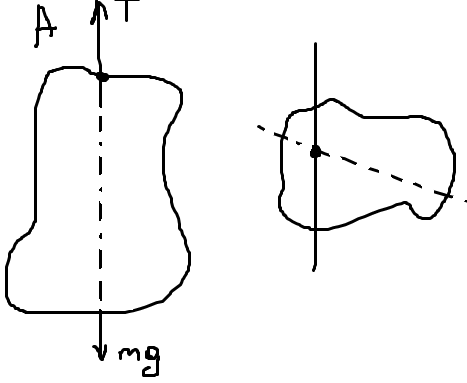
10 Понятие центра массы тела и методика определения
Центр
масс, центр
инерции, геометрическая точка, положение
которой характеризует распределение
масс в теле или механической системе.
Координаты Ц. м. определяются формулой:

М етоды
определение ЦМ:
етоды
определение ЦМ:
разбиение Тв т на элементы ЦМ которых нам известны
М етод
нулевого момента масс:
етод
нулевого момента масс:
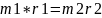
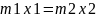

метод компенсирующих масс(по 2 методу)


4)Экспериментальный
метод: подвесить несколько раз. На одной
линии, тк тело находится в состоянии
покоя когда
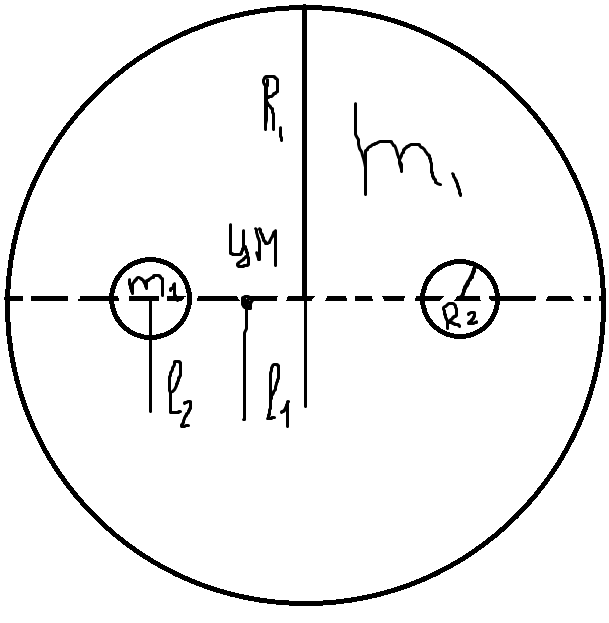
11,Момент инерции тел, пример его определения. Теорема Штейнера
Момент инерции - величина, характеризующая распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении.
Момент
инерции тела относительно оси вращения
зависит от массы тела и от распределения
этой массы. Чем больше масса тела и чем
дальше она отстоит от воображаемой оси,
тем большим моментом инерции обладает
тело. Момент инерции элементарной
(точечной) массы
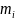 ,
отстоящей от оси на расстоянии
,
отстоящей от оси на расстоянии
 ,
равен:
,
равен:

Момент инерции всего тела относительно оси равен:

или, для непрерывно распределенной массы:

Момент инерции всего тела сложной конфигурации обычно определяют экспериментально. Вычисление моментов инерции во многих случаях можно упростить, используя соображения симметрии и теорему Штейнера.

Это
важное геометрическое соотношение
называется теоремой Гюйгенса-Штейнера.
Момент инерции тела относительно
какой-либо оси равен моменту инерции
его относительно параллельной оси,
проходящей через центр масс, сложенному
с величиной
 где
где
 расстояние между осями.
расстояние между осями.
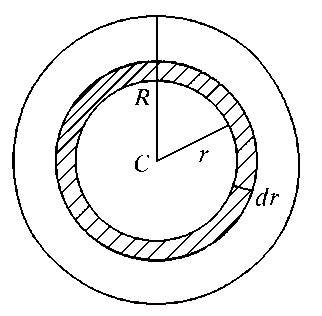 Вычислим
в качестве примера момент инерции
однородного диска относительно оси,
перпендикулярной к плоскости диска и
проходящей через его центр.
Вычислим
в качестве примера момент инерции
однородного диска относительно оси,
перпендикулярной к плоскости диска и
проходящей через его центр.
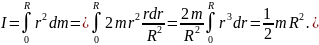
12 Методика сложения сил, прилож-х к разл-м точкам тела и определения их вклада в изменение состояния дв-я
В большинстве случаев на тело действует несколько сил,приложенных к телу, действие кот-х можно заменить одной силой, равной по своему действию этим силам. Сила, кот-я производит на тело, такое же действие, как несколько одновременно действующих сил, наз-ся равнодействующей(равнодей-й) этих сил.Нахождение равнодей-й этих сил наз-ся сложением этих сил или нахождение их суммы. Слагаемые силы наз-ся составляющими силами.
А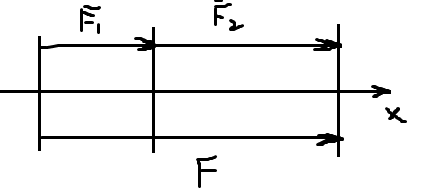 )
найдем равнодей-щую двух сил, действующих
на тело по одной прямой в одну сторону.
Пусть
)
найдем равнодей-щую двух сил, действующих
на тело по одной прямой в одну сторону.
Пусть
Т.о. равнодей-я сил, направл-х по одной прямой в одну сторону, направлена в ту же сторону, а ее модель равен сумме модулей составляющих сил.
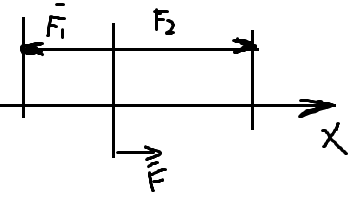
Б) пусть силы действуют на тело по одной прямой, но в противоположные стороны.

равнодей-я всех сил, напр-на в сторону большей силы, а ее модуль равен разности модулей составляющих сил.
В) тело под действием двух равных и противоположно направленных сил будет в покое или двигаться равномерно и прямолинейно так:


Г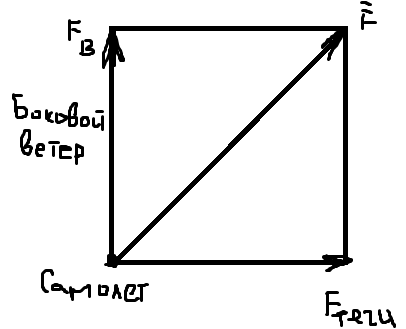 )
Если силы направлены под векторным
углом, сложение производится по правилу
параллелограма
)
Если силы направлены под векторным
углом, сложение производится по правилу
параллелограма


Теорема Пифагора
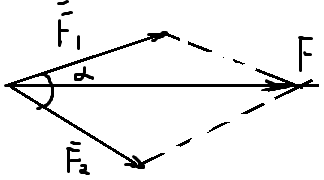

Теорема косинусов
