2.1.2. Способы задания движения точки

Существует три способа: естественный, координатный, вектор­ный .

Естественный способ задания дви­жения точки. Если кроме траектории, на которой отмече­но начало отсчета 0, задана зависимость

между расстоянием S и временем t , это уравнение называется за­коном движения точки по заданной траектории.

Пример:

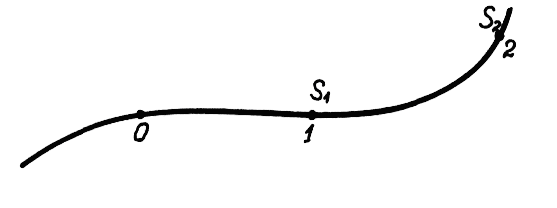
Пусть, например, задана некоторая траектория, движение точки по которой определяется уравнением . Тогда в момент времени , т.е. точка находится в начале отсчета 0; в момент времени точка находится на расстоянии ; в момент времени

точка находится на расстоянии от начала отсчета 0.

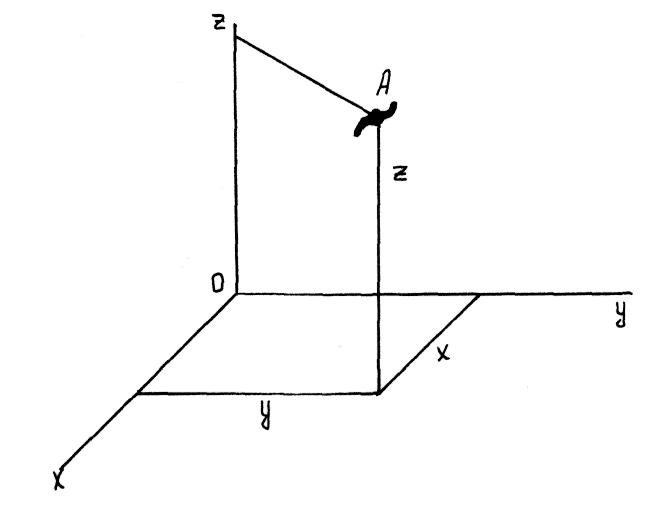
Координатный способ задания дви­жения точки. Когда траектория точки заранее не извест­на, положение точки в пространстве определяется тремя координа­тами: абсциссой X, ординатой У и аппликатой Z .

или , исключив время.

Эти уравнения выражают закон движения точки в прямоугольной системе координат (OXYZ).

В частном случае, если точка движется в плоскости, закон дви­жения точки выражается двумя уравнениями:

или .

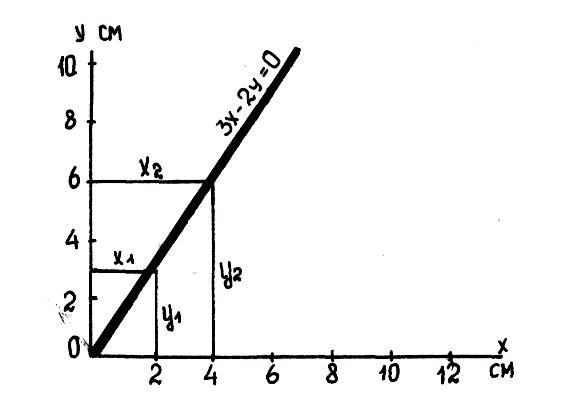
Например. Движение точки в плоской системе координат задано уравнениями X = 2t и У=3t (X и У - см, t - с). Тогда в момент времени и у_о = 0, т.е. точка находится в начале координат; в момент времени координаты точки , ; в момент времени координаты точки ,

и т.д.

Зная закон движения точки в прямоугольной системе координат, можно определить уравнение траектории точки.

Например, исключив время t из заданных выше уравнений X = 2t и У = 3t, , получим уравнение траектории ЗХ - 2У = 0. Как видим, в этом случае точка движется по прямой, проходящей через начало координат.

2.1.3. Определение скорости точки при естественном способе задания ее движения

Пусть движение точки А по заданной траектории происходит со­гласно уравнению , требуется определить скорость точки в момент времени t

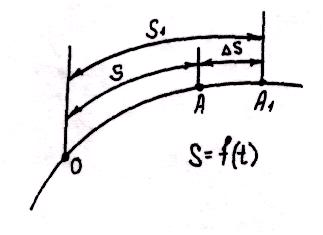t - положение точки А;

- положение точки A₁

- путь .

За промежуток времени точка прошла путь ,

значение средней скорости на этом пути

,

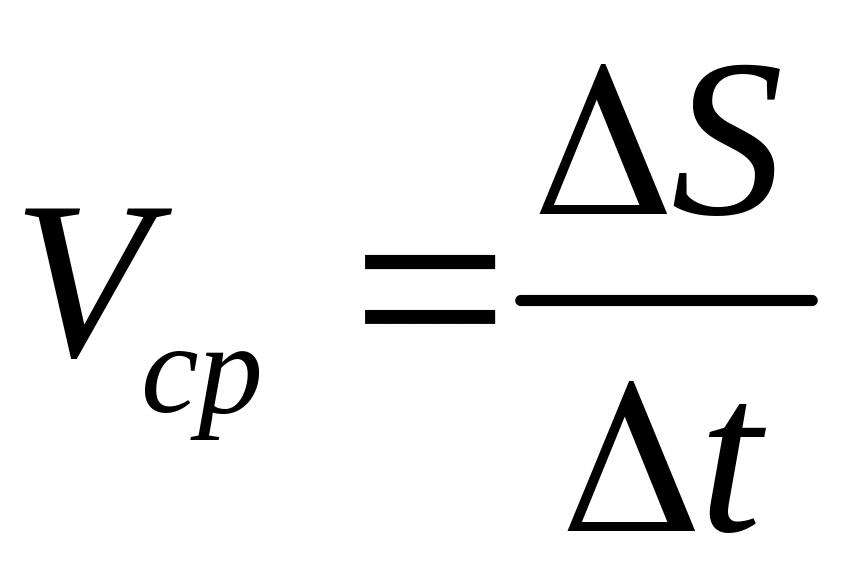но оно отличается от значения скорости в момент времени t . Скорость в заданный момент t

,

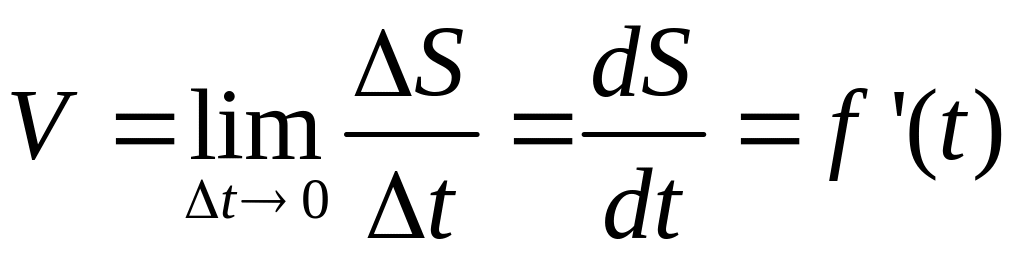т.е. значение скорости точки, движение которой задано естествен­ным способом, в любой момент времени равно первой производной от расстояния (дуговой координаты) по времени.

Направление скорости, как отмечалось выше, известно заранее.

2.1.4. Определение ускорения точки при естественном способе задания ее движения

Вектор - ускорение точки в данный момент - есть геометри­ческая сумма касательного и нормального ускорений:

.

Вектор в любой момент времени направлен по касательной, поэтому вектор называется касательным, или тангенциальным ускорением. Модуль каса­тельного ускорения

равный производной от скорости в данный момент по времени или, иначе, второй производной от расстояния по времени, характеризу­ет быстроту изменения значения скорости.

Доказано, что вектор в любой момент времени перпендикуля­рен касательной, поэтому он называется нормальным ускорением.

.

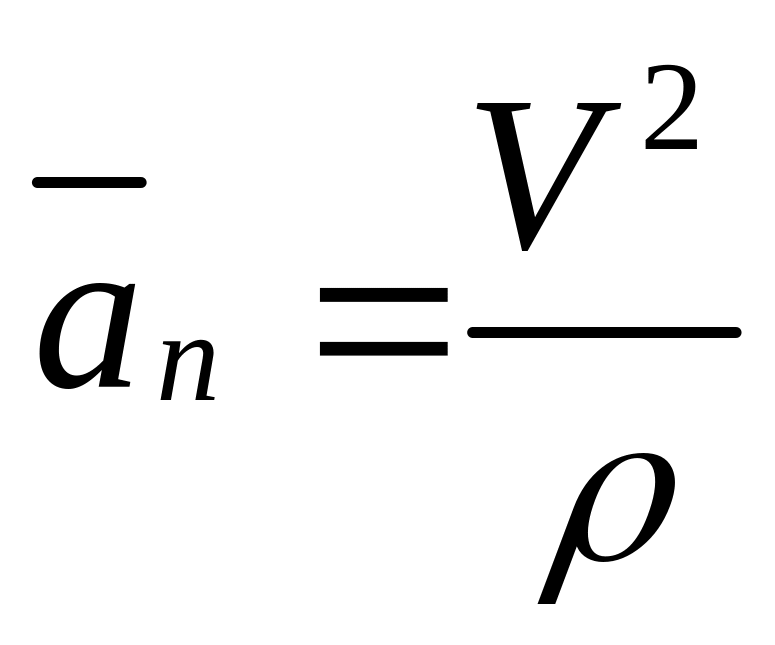Значит, модуль нормального ускорения пропорционален второй степени модуля скорости в данный момент, обратно пропорционален радиусу кривизны траектории в данной точке и характеризует быст­роту изменения направления скорости.

Модуль ускорения

,

а направление a (угол ) находим с помощью тригоно­метрических функций по одной из следующих формул:

.

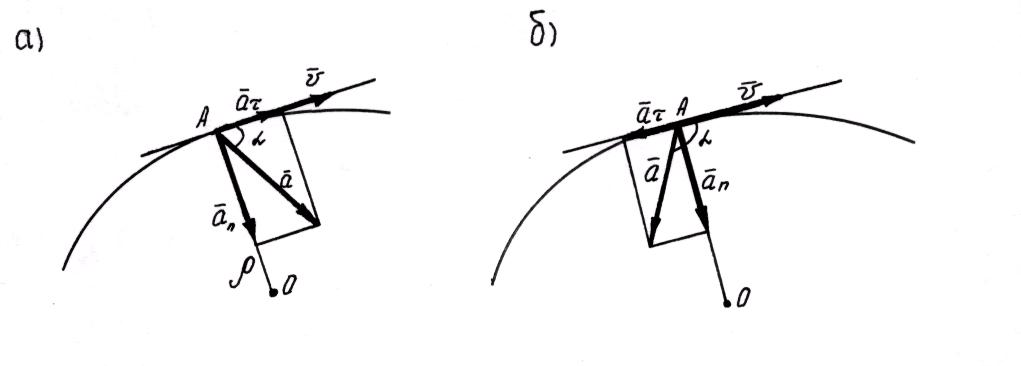
Если векторы и направлены в одну и ту же сторону (a), то движение точки называется ускоренным. При этом зна­чения и имеют одинаковые знаки ( или ). Если же векторы и направлены в противоположные стороны ( ), то движение точки называется замедленным. В этом случае знаки и разные ( или ).