7.Метод эквивалентного генератора:

В любой электрической схеме можно мысленно выделить какую-то одну ветвь, а всю остальную часть схемы, независимо от структуры и сложности, условно изобразить прямоугольником, который представляет собой так называемый двухполюсник.

Таким образом, двухполюсник - это обобщённое название схемы, которая двумя выходными зажимами (полюсами) присоединена к выделенной ветви. Если в двухполюснике есть источник Э.Д.С. или тока, то такой двухполюсник называют активным. Если в двухполюснике нет источника Э.Д.С. или тока, то его называют пассивным.

При решении задачи методом эквивалентного генератора (активного двухполюсника) необходимо:

1) Мысленно заключить всю схему, содержащую Э.Д.С. и сопротивления, в прямоугольник, выделив из нее ветвь аb, в которой требуется найти ток (рис 2.13).

2 ) Найти напряжение на зажимах разомкнутой ветви ab (в режиме холостого хода).

Напряжение холостого хода Uо (эквивалентное Э.Д.С. Еэ) для рассматриваемой цепи

можно найти так:

Сопротивление R4 в расчёт не вошло, так как при разомкнутой ветви ab ток по нему не протекает.

3)Найти эквивалентное сопротивление. При этом источники Э.Д.С. закорачиваются, а ветви, содержащие источники тока, размыкаются. Двухполюсник становится пассивным.

Д ля данной схемы

4) Вычислить значение тока. Для данной схемы имеем:

8.Синусоидальные напряжения и токи. Мгновенные, амплитудные, действующие и средние значения синусоидальных величин.

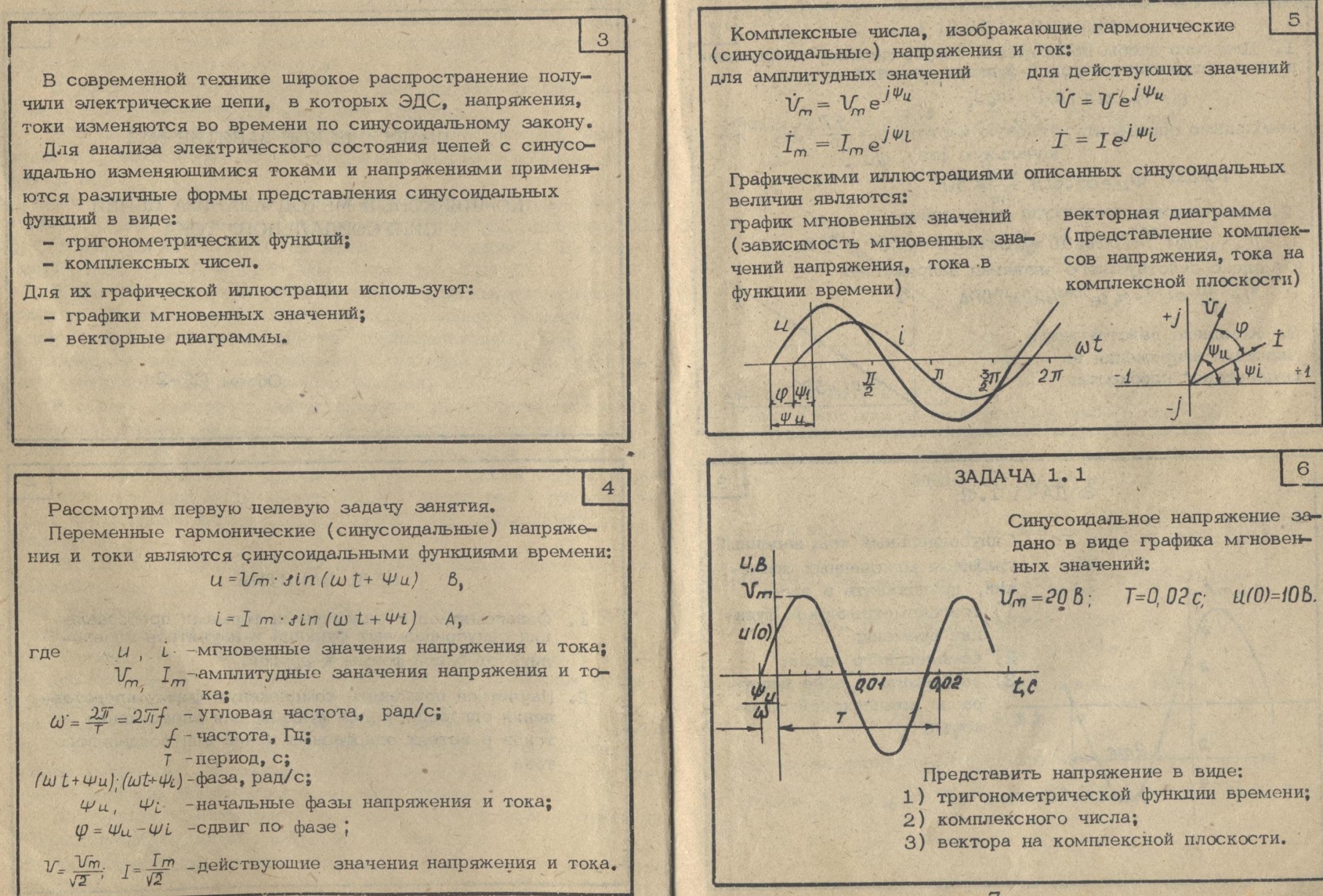
Переход от показательной формы к алгебраической: Vm=20e^(j30)=20*cos(30)+j20*sin(30). Ну а просто V-т.е. действующее значение будет: (20/Sqrt(2))*e^(j30).

9.Комплексная, тригонометрическая, векторная и волновая формы представления синусоидальных величин.

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами. Далее  Смотри предыдущий вопрос.

10.Комплексный метод расчета цепей с синусоидальными режимами. Баланс Мощностей:

При расчетах установившихся режимов линейных электрических цепей синусоидального тока мгновенным значениям синусоидальных функций времени ставят в соответствие комплексные мгновенного значения. Например, для тока комплексные мгновенного значение имеет вид

Комплексное число называют комплексным амплитудным значением или комплексной амплитудой, а – комплексным действующим значением тока.

===Аналогично определяются комплексные мгновенные значения синусоидальных напряжений, э. д. с

Так напряжению соответствуют =комплексные мгновенные значения

= комплексные амплитуды

= и комплексные действующие значения

БАЛАНС МОЩНОСТЕЙ:

11.Резонанс напряжений. Условие, признаки, резонансные кривые, применение.

Для данной цепи имеет место резонанс напряжений.

Условие резонанса напряжений ; (фи)=0;

При резонансе напряжений или режимах, близких к нему, ток в цепи резко возрастает. В теоретическом случае при R=0  его величина стремится к бесконечности. Соответственно возрастанию тока увеличиваются напряжения на индуктивном и емкостном элементах, которые могут во много раз превысить величину напряжения источника питания.

=== Отношение активной мощности к реактивной есть коэффициент активной мощности. cos(фи)=P/S; Он показывает, какая доля активной мощности содержится в полной. Он изменяется от 0 до 1.

Резонанс-явление, возникающее при подсоединении реактивных элементов различного характера, при котором наблюдается совпадение начальной фазы напряжения и тока.

Резонансными кривыми называются зависимости тока и напряжения от частоты.

Важной характеристикой резонансного контура является добротность Q, определяемая отношением напряжения на индуктивном (емкостном) элементе к входному напряжению:

1)Если XL >Xcрезонанс называется активно-индуктивный. 0<(фи)<((пи)/2)

2)Если XL <Xc Резонанс активно-емкостной. -((пи)/2)<(фи)<0

j j

UL

Uвх UL

I I

1 ) 1 2. 1

Uc UR UR

Uвх

Явление резонанса находит полезное применение на практике, в частности в радиотехнике. Однако, если он возникает стихийно, то может привести к аварийным режимам вследствие появления больших перенапряжений и сверхтоков.

Физическая сущность резонанса заключается в периодическом обмене энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, причем сумма энергий полей остается постоянной.