
- •2. Уравнения Максвелла в дифференциальной и интегральной формах.
- •3. Полный ток и его составляющие
- •4. Классификация сред, материальные уравнения
- •5. Граничные условия для электромагнитного поля. Нормальные и тангенциальные составляющие векторов
- •6. Закон Джоуля-Ленца в дифференциальной и интегральной формах.
- •7. Общее уравнение баланса энергии в электромагнитном поле.
- •8. Уравнения Максвелла для электростатического поля
- •9. Электростатический потенциал. Граничные условия в электростатике
- •11. Уравнения Максвелла в символической форме. Комплексные диэлектрическая и магнитная проницаемости среды.
- •13. Плоские однородные волны в поглощающих средах.
- •14.Поляризация плоских волн
- •15. Нормальное падение плоской волны на границу раздела двух сред. Формулы Френеля
- •16. Наклонное падение плоских волн на границу раздела двух сред. Формулы Френеля для горизонтально и вертикально поляризованных волн.
- •18. Наклонное падение плоских электромагнитных волн на границу с диэлектриком. Угол Брюстера
- •19. Наклонное падение плоских электромагнитных волн на границу поглощающей среды. Приближенные граничные условия Леонтовича
- •17. Наклонное падение плоских электромагнитных волн на границу с диэлектриком. Плоские неоднородные волны
- •20. Понятие о направляющей системе. Классификация направляемых волн
- •21. Условия распространения электромагнитных волн в направляющих системах. Критическая частота, критическая длина волны.
11. Уравнения Максвелла в символической форме. Комплексные диэлектрическая и магнитная проницаемости среды.

Где
 - комплексные амплитуды векторов поля
- комплексные амплитуды векторов поля


Сократив на избавимся от временной зависимости и перейдем к комплексным амплитудам:


 -
комплексная
диэлектрическая проницаемость
-
комплексная
диэлектрическая проницаемость

Относительная характеризует проводимые свойства среды(проводящие св-ва среды)
Обозначим
 ,
,
 тогда
тогда
Отншение
 - тангенс
угла диэлектрических потерь
- тангенс
угла диэлектрических потерь
Если tg>0- то диэлектрик
Если tg<45 – то это проводник
Мнимая
часть комплексной диэлектрической
проницаемости характеризует ток
проводимости и электрические потери в
веществе: если потерями можно пренебречь,
то
 =0.
=0.
Аналогично
получим:
 (учитывает
магнитные потери)
(учитывает
магнитные потери)
 -потери на перемагничивание(способность
среды намагничиваться)
-потери на перемагничивание(способность
среды намагничиваться)
Уравнение Максвелла, таким образом, будут иметь вид:
для комплексных векторов:


для комплексных амплитуд

Эти уравнения дополняются еще двумя:
divE = 0, divH = 0.
12. Волновые уравнения и их решение. Плоские однородные волны в не поглощающих средах.
Получим из уравнений Максвелла уравнения отдельно для E и отдельно для H

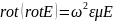

Обозначит
 ,
где
,
где
 – волновое
число
– волновое
число
Так как divE=0, то

Проведем аналогичные действия относительно вектора H
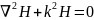
это уравнения Гельмгольца.
Для комплексных амплитуд они выглядят следующим образом:


Плоская волна – это волна, фронт которой представляет собой плоскость.
Предположим, что в точке О находится точечный источник. Плоскость Р перпендикулярна Oz. При перемещении в плоскости Р не происходит изменения состояния процесса. Так как состояние процесса во всех точках плоскости одинаково, то эту плоскость можно назвать фронтом волны. В этой плоскости при перемещении в перпендикулярном оси Z направлении не происходит никаких изменений. Что математически означает следующее:

Такое приближение называется приближением плоской волны. В этом случае трехмерные уравнения преобразуются в одномерные уравнения:


Решение подобного рода волновых уравнений хорошо известно и имеет вид:


 – орты,
показывающие
направление векторов электрического
и магнитного полей
– орты,
показывающие
направление векторов электрического
и магнитного полей
Переходя от комплексных векторов к их реальным частям, получим:


Отношение
 называется фазовой скоростью и показывает
скорость распространения волнового
фронта электромагнитной волны.
называется фазовой скоростью и показывает
скорость распространения волнового
фронта электромагнитной волны.
Для вакуума фазовая скорость будет:
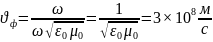
Это означает, что в вакууме скорость распространения электромагнитной волны равна скорости света. Определим расстояние l между точками поля с фазами, отличающимися
на 360 градусов.

Длина волны в вакууме

Фазовая
скорость в остальных средах и
соответственно, длина волны
и
соответственно, длина волны
 .Как
следует из формулы для фазовой скорости,
она не зависит от
.Как
следует из формулы для фазовой скорости,
она не зависит от
частоты, значит вакуум среда не дисперсионная.
Установим связь между направлениями векторов электрического и магнитного полей. Начнем с уравнений Максвелла:
Заменяем векторные уравнения скалярными

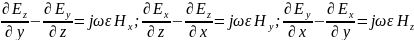
Учтем
, что

Тогда


видно,
что у плоских волн нет продольных
составляющих, т.к. .
.
Составим скалярное произведение (E,H) , выразив Еx и Еy


Так как скалярное произведение векторов равно нулю, векторы E и H в плоской волне перпендикулярны друг другу. Поскольку у них нет продольных составляющих, то E и H перпендикулярны направлению распространения волны. Найдем отношение амплитуд векторов электрического и магнитного полей.
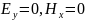
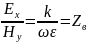

где – волновое сопротивление среды с макроскопическими параметрами и .
Величина
 называется волновым сопротивлением
вакуума.
Оно
равно 377 Ом.
называется волновым сопротивлением
вакуума.
Оно
равно 377 Ом.
На основе анализа решения волновых уравнений можно сделать
следующие выводы:
1.В
вакууме плоские волны распространяются
со скоростью света, в остальных
диэлектрических средах скорость меньше
в раз.
раз.
2.Векторы электрического и магнитного полей не имеют продольных составляющих и перпендикулярны друг другу.
3.Отношение амплитуд электрического и магнитного полей равно волновому сопротивлению среды, в которой происходит распространение электромагнитных волн.
