9. Электростатический потенциал. Граничные условия в электростатике

Начнем с первого из записанных уравнений, утверждающего, что электростатическое поле является безвихревым (ротор его напряженности равен нулю), или, как чаще говорят, потенциальным. Происхождение второго термина связано со следующим свойством электростатического поля. В силу известного тождества векторного анализа

rotgrad0

напряженность этого поля Е есть градиент некоторого скаляра , который называется электростатическим потенциалом. Принято писать

E = -grad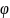

или в декартовых координатах

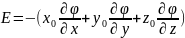
Потенциал- неоднозначная функция поля. Если положить

E = -grad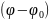

где 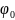- некоторый скаляр,будет видно что записанное выражение будет описывать поле

Сила поля совершает работу :

A El ,

А работа по переносу заряда из точки М1 в точку М2 есть

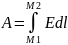
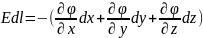
видим, что он представляет собой взятый с обратным знаком полный дифференциал функции :

Edl d

Следует что,

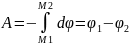
Итак, работа, совершаемая полем при перемещении положительного, единичного точечного заряда в электростатическом поле, равна разности потенциалов начальной и конечной точек пути. Она не зависит от абсолютного значения потенциалов, а также от вида пути, соединяющего точки. В частности, работа при обходе замкнутого контура равна нулю.

связь разности потенциалов с напряженностью поля:

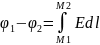
В электростатике обычно принимают, что потенциал в бесконечно удаленных точках равен нулю. Тогда потенциал в произвольной точке М численно равен работе, совершаемой при перемещении единично го заряда из этой точки в бесконечность,

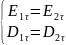- граничные условии для векторов

Рассмотрим границу идеальный диэлектрик - проводник.

-граничные условия для векторов электрического поля

Поле в металле равно нулю. grad =0, следовательно, на поверхности проводника = const. Проводящие поверхности в электростатике эквипотенциальны.

10. Уравнения для электростатического потенциала. Теорема единственности

Получим из уравнений Максвелла для векторов электрического поля уравнения для электростатического потенциала.

divD = p

Используя материальное уравнение D E получим divE , и так как

E grad, то

divgrad

Если не зависит от координаты, то есть среда однородна, то

divgrad

Так как , можно записать

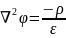
Это уравнение Пуассона.

Если 0 , получим

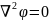
Это уравнение Лапласа.

Основная задача электростатики заключается в следующем: задана система заряженных тел. Требуется найти распределение потенциала в пространстве, окружающем эти тела, представляющем собой идеальный диэлектрик. Однако очень часто задается не распределение заряда, а полные заряды либо потенциалы заряженных тел.

Сформулируем теперь теорему единственности. Основная задача электростатики решается единственным образом, если:

а) потенциал есть непрерывная, конечная, однозначная функция координат;

б) на бесконечном расстоянии от исследуемой системы заряженных тел потенциалы и заряды равны нулю;

в) поверхности проводящих тел эквипотенциальны;

г) заданы либо потенциалы проводящих тел, либо их заряды.