
- •«Геодезия и картография локальный комплекс наук обеспечивающий основу гис. Предмет и задачи курса системы координат в гис.»
- •3.Эллипсоид вращения - как геометрическая модель Земли, его параметры, принципы их определения и ориентирования эллипсоида в теле земли.
- •5. Криволинейная эллипсоидальная система геодезических координат в,l,h ее характеристика и свойства.
- •1 2. Преобразование пространственной прямоугольной системы координат – X, y, z в эллипсоидальные геодезические – b, l, h.
- •1 3. Топоцентрические системы пространственных прямоугольных координат – xt, yt, zt, и их характиристики.
- •20. Понятие о проекциях эллипсоида на плоскость. Проекция Гаусса-Крюгера, её свойства. Система зон и условные ориентиры.
- •21.Геометрическая интерпретация проектирования геодезических построений с эллипсоида на плоскость в проекции Гаусса
- •24. Преобразование плоских прямоугольных координат Гаусса-Крюгера из одной зоны в другую.
1 2. Преобразование пространственной прямоугольной системы координат – X, y, z в эллипсоидальные геодезические – b, l, h.
Связь пространственных прямоугольных координат Х, У, Z с эллипсоидальными геодезическими координатами B, L, H можно легко установить на основании рис. 3.7.
Проведем через точку Q, не лежащую на поверхности эллипсоида, нормаль Qn, и, обозначая отрезок On через d, будем иметь: Qn=N+H;
d=e2 N sin B; Q0n=(N+H) cos B;
И тогда формулы связи прямоугольных пространственных координат с эллипсоидальными геодезическими координатами можно записать в окончательном виде :
X=(N+H) cos B cos L;
Y=(N+H) cos B sin L; Z=(N+H) sin B-d= [N(1-e2)+H] sin B.
При обратном переходе: от пространственных прямоугольных координат – Х, У, Z к эллипсоидальным геодезическим координатам B, L, H можно получить замкнутую, строгую формулу только для вычисления долготы L
L=arctg
и вспомогательной величины
D=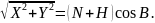
Вычисление же широты может быть выполнено только методом последовательных приближений по формуле
B=
arctg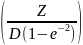
где
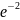 =
=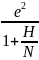 (3.28)
(3.28)
В
первом приближении следует принять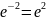 , во втором и далее величина должна уже
определяться по формуле (3.28), с
предварительным вычислением Н
по
формуле (3.29) и N
–
по формуле Ni=
, во втором и далее величина должна уже
определяться по формуле (3.28), с
предварительным вычислением Н
по
формуле (3.29) и N
–
по формуле Ni=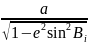 (i=1,
2), используя широту, полученную в
предыдущем приближении. Имея широту,
вычисляют высоту:
(i=1,
2), используя широту, полученную в
предыдущем приближении. Имея широту,
вычисляют высоту:
H=D sec B – N (3.29)
1 3. Топоцентрические системы пространственных прямоугольных координат – xt, yt, zt, и их характиристики.
Предположим, что начало топоцентрической СК располагается в точке , эллипсоидальные геодезические координаты которой В0, L0, H0.
Для установления связи между пространственными декартовыми топоцентрическими горизонтными XT, YT, ZT и пространственными прямоугольными координатами Х, У, Z сначала перенесем начало координат топоцентрической системы в точку n (рис). Тогда, при неизменности направления осей топоцентрической системы, будем иметь частично преобразованную систему топоцентрических координат X1T, Y1T, Z1T:
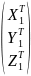 =
=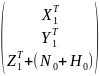
Теперь осуществим разворот осей только что преобразованной системы топоцентрических координат X1T, Y1T, Z1T вокруг оси nZT на угол 900-B0 , чтобы ось nZT совпала с осью вращения эллипсоида. Получим вторично преобразованную систему топоцентрических координат X2T, Y2T, Z2T:
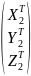 =
=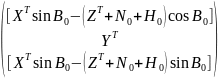
После этого перенесем начало координат системы X2T, Y2T, Z2T в центр эллипсоида О на расстояние On =e2 N0 sin B0 , при этом направление осей остается неизменным.
Очевидно,
в этом случае изменится только одна
координата Z2T
, т. е.
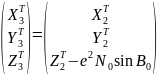 Наконец,
оси координат, лежащие теперь в плоскости
экватора, повернем
Наконец,
оси координат, лежащие теперь в плоскости
экватора, повернем
вокруг
оси OZ (
O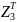 )
на угол, равный долготе L0
начальной
точки Q0
,
а у
)
на угол, равный долготе L0
начальной
точки Q0
,
а у
абсциссы
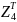 изменим
знак на обратный (так как система ОХУZ
– правая, а
изменим
знак на обратный (так как система ОХУZ
– правая, а
система Q0 XT, YT, ZT – левая), в результате преобразования получим
P=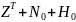
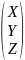 =
=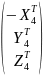 =
=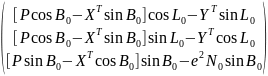
Обратный переход от X, У, Z к XT, YT, ZT
Чтобы
найти обратные зависимости, решим
уравнения (3.49) относительно XT,
YT,
ZT.
В
результате решения получим
R=Z+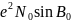 ;
S=(X
cos
;
S=(X
cos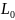 + Y
sin
+ Y
sin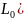 ;
XT=R
cos
;
XT=R
cos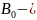 S
sin
S
sin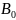 ;
YT=Y
cos
;
YT=Y
cos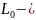 X
sin
;
ZT=R
sin
X
sin
;
ZT=R
sin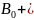 S
cos
(
S
cos
(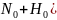 .
.
