Лабораторна робота №6 Чисельні та символьні методи обчислень
1 Мета роботи
Навчитися проводити числове та символьне інтегрування та диференціювання функцій, розв’язувати системи диференційних рівнянь у числовій та символьній формах, проводити операції над поліномами, застосувати зворотне перетворення Лапласа, проводити апроксимацію функцій.
2 Завдання на лабораторну роботу
2.1 Ознайомитись зі змістом пункту 3 методичних вказівок.
2.2 Провести числове та символьне інтегрування та диференціювання функцій згідно індивідуального завдання (Додаток до лабораторної роботи).
2.3 Використати різні засоби для розв’язання систем диференційних рівнянь, що описують роботу ДПС згідно вказівкам викладача.
2.4 Самостійно задати поліноми і провести з ними дії, аналогічні описаним у п. 3.3.
2.5 Отримати та проаналізувати перехідну характеристику системи згідно п. 3.4 та вказівкам викладача.
2.6 Скласти звіт, відповісти на контрольні питання.
3 Основні теоретичні відомості
3.1 Числове інтегрування та диференціювання функцій
Для знаходження значення означеного інтеграла в середовищі пакета передбачена функція quad, яка розраховує значення інтеграла F(Х) в діапазоні від А до В з допустимою точністю 1е-3 використовуючи метод Сімпсона. Приклад виклику цієї функції такий
q= quad (' F ', a, b),
де ' F ' - текстова змінна (назва файла, в якому зберігається підінтегральна функція).
Розглянемо приклад знаходження значення означеного інтеграла
Опис підінтегральної функції запишемо у файлі з назвою 'integ, що має вигляд
function F=integ(х)
F=х;
Тоді, записавши в командній стрічці пакета вираз
Q=quad('integ', 0, 3),
отримаємо значення інтеграла: Q = 4.5000
Окрім цієї функції для розв'язування задачі знаходження значення визначеного інтеграла в пакеті передбачено функцію quad8, яка реалізує рекурсивну адаптивну восьми-точкову формулу Ньютона-Котеса. Ця функція дає кращі результати для обчислення значення означеного інтеграла, підінтегральна функція якого має певні особливі точки на інтервалі інтегрування.
Для визначення наближеного значення похідної необхідно знайти різницю між сусідніми значеннями числово заданої функції. Цю операцію виконує diff. Якщо х є вектором, то результатом виконання команди diff (х) буде вектор |х(2)-х(1)-х(3)-х(2) ... х(n)-х(n-і)|. У випадку, якщо х є матицею, то результатом виконання команди diff (х) буде матриця [х(2:n,:) -х(1:n-1,:)]. Наприклад,
diff ((1:10).^2)
ans =
З 5 7 9 11 13 15 17 19
Якщо вектори х та у складаються з координат точок кривої, то наближене значення похідної отримується з виразу
dydx=diff (y)./diff(х)
3.2 Розв'язування систем диференціальних рівнянь
Деякі дії Маtlab дозволяє виконати в символьному вигляді, для чого застосовується розширення пакету Symbolic Math Toolbox.
Під символьним об’єктом тут розуміється змінна, призначена для символьних перетворень. Об’ява такої змінної виконується функцією sym або syms.
Sym. Ця функція використовується при об’яві якої-небудь однієї змінної символьною, наприклад
Sym x ; % об’ява символьної змінної x
Sym y ; % об’ява символьної змінної y
Тепер над цими змінними x та y можна проводити символьні перетворення. Наприклад, щоб спростити заданий вираз, використовується функція simplify
>> sym x ;
>> sym y ;
>> simplify ((x^2-y^2)/(x-y))
ans =
x+y
Syms. Дана функція дозволяє об’явити кілька символьних змінних разом, які потрібно відділити одне від одного пробілами, наприклад
>>syms x y z
Крім функції simplify, для спрощення можна використати функцію expand, формат виклику якої має вигляд
Rez=expand (s)
де s – символьний вираз, що потрібно спростити,
rez – результат дії, наприклад
>> syms x y ;
rez=expand(sin(x+y))
rez=sin(x)*cos(y)+cos(x)*sin(y)
У символьному вигляді можна провести і операцію диференціювання за допомогою тієї ж функції diff, попередньо зробивши об’яву символьних змінних.
Наприклад
>> syms x y ;
>> D=diff(x^2+4*x^5)
D=
2*x+20*x^4
Функцію можна задати попередньо, наприклад
syms x y ;
S=x^3*y^2+sin(x*y) ;
D=diff(s,’x’,2)
D=6*x*y^2-sin(x*y)*y^2
Зверніть увагу, що тут вираз диференціюється двічі, тому що загальний вигляд виклику функції дозволяє це:
D=diff(s,’v’,n) ,
де s – вираз, що диференціюється,
v – змінна диференціювання,
n – кількість диференціювань (якщо диференцюєм один раз, можна не вказувати).
Інші потрібні функції можна розглянути за допомогою довідкової системи MatLab.
Далі буде розглянуто чисельні методи розв’язування диференційних рівнянь. Але в деяких випадках це також можна зробити за допомогою символьної математики. Так, використовуючи функцію dsolve, яка має такі формати звернення
1. y=dsolve(‘Dy(x)’)
де Dy(x) – рівняння,
y – рішення
2. y=dsolve(‘Dy(x)’,’ПУ’)
де ‘ПУ’ – початкові умови.
За допомогою dsolve можна розв’язувати і системи диференційних рівнянь. При цьому вона має такий формат звернення
[f, a]=dsolve(‘Df(x), Da(x)’,’ПУ’)
де Df(x) та Df(y) – система рівнянь.
Приклад. Розв’язати диференційне рівняння y’(x)=0.6-0.2y(x) з початковою умовою y(0)=0
>> y=dsolve(‘Dy+0.2*y-0.6=0’,’y(0)=0’)
y=
3-3*exp(-1/5*t)
У середовищі пакета Маtlab до недавнього часу були доступні тільки дві функції для розв'язування системи диференційних рівнянь: ode23 та ode45, що реалізували відповідно формули Фельберга другого та четвертого порядків. Спосіб виклику обох функцій є ідентичним. Так, наприклад, для розв'язування системи диференційних рівнянь в інтервалі часу [t0, tk] з початковими умовами, визначеними вектором xо, виклик функції має вигляд
[t, х] = ode23 ( ' fileode ', tint, х0, options) ,
[t, х] = ode 45 (' fileode', tint, х0 ),
де tint=[tstart tfinish].
Параметр options - визначається за допомогою odeset. Наприклад,
options = odeset ('RelTol' , 1е-4,'АbsТоl', [1е-4 1е-4 1е-5]);
задає допустиму точність 1е-4 і абсолютну точність 1е-4 для двох перших координат і 1е-5 – для третьої. Текстова змінна fileode визначає назву функціонального файла, в якому записана система диференціальних рівнянь у нормальний формі Коші. Структура такого файла має вигляд
function F=xmotor (t, x)
f (1) = f1(t, x);
…
f (n) =fn (t, x);
F = [f (1);…;f (n)]
причому необхідно зазначити, що назва функційного файла може бути будь-якою.
Окрім описаних вище методів розв’язування систем диференційних рівнянь в середовищі пакета, починаючи з версії 4.2с запропоновані такі нові функції:
ode113 – реалізує метод прогноз – корекція за формулами Адамса-Башфорта-Мултона;
ode23s – реалізує метод Розенброкка;
ode15s – реалізує метод диференціювання назад, що побудований на використанні сімейства формул числового диференціювання Klopfenstein-Shampine порядку 1-5. (призначені для розв’язування жорстких систем);
ode23t – реалізує метод трапецій;
ode23іtb – реалізує метод TR-BDF2, що подібний до методу Рунге-Кутта, в якому на першому кроці застосовується формула трапецій (ТR), а на другому – формули диференціювання назад (ВDF) другого порядку.
Як приклад розглянемо розв'язування системи рівнянь, що описують пуск двигуна постійного струму незалежного збудження із заданими параметрами. Перехідні процеси в колі збудження до моменту пуску вже завершились, а момент статичного навантаження нульовий. Тоді файл, в якому записана система рівнянь, що описує двигун незалежного збудження, матиме вигляд
function F=motode (t, у)
дані двигуна
U=220.0; I=15; w=314.15;
r=1.3; рn=2; J=0.3;
L=0.6*U/(I*w*рn) ;
с=(u-I*r)/w;
формування матриць коефіцієнтів
А=[-r/L, -с/L; с/J 0]; В=[1/L.;0];
знаходження похідних
F=А*у+B*U;
Головна програма для розв'язування поставленої задачі може бути записана так:
tint=[0 8];
у0=[0 0]' ;
[t, у]=ode 45( 'motode' , tint, у0) ;
subplot (211), рlot (t, у(:,1)), х1аbе1(' t '), у1аЬе1(' і (t) ' ), grid;
subplot (212), рlot (t, у(:,2)), х1аbе1(' t '), у1аЬе1(' w (t) ' ), grid.
Результатом роботи цієї програми буде вивід графіків зміни струму та швидкості обертання вала двигуна (рис. 6.1).
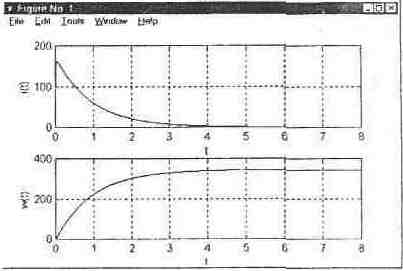
Рисунок 6.1 - Вигляд вікна виводу графіків зміни струму та швидкості обертання вала двигуна постійною струму незалежного збудження під час пуску.
Реалізація набору функцій для розв'язування систем диференційних рівнянь дає змогу користувачеві досліджувати динамічні режими в будь-яких електричних колах, описаних за допомогою системи диференційних рівнянь.