3 Решение однофазной линейной электрической цепи переменного тока

3.1 Схема замещения электрической цепи, определение реактивных сопротивлений элементов цепи

К зажимам электрической цепи, схема замещения которой приведена на рисунке 3.1, подключен источник синусоидального напряжения

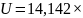
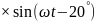В, с частотой 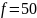Гц.

Дано:

; ;

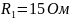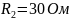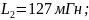
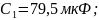
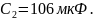
Определить: .

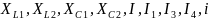Рассчитаем реактивные сопротивления элементов цепи:

;

;

;

.

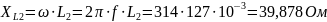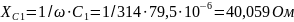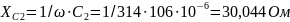Находим комплексные сопротивления ветвей, затем участков цепи и всей цепи:

;

;

;

;

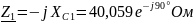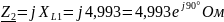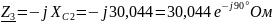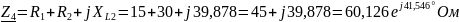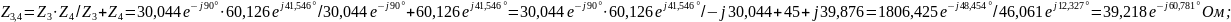
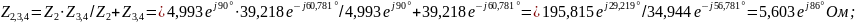
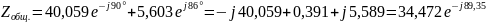
Выразим действующее значение напряжений в комплексной форме:

.

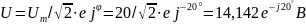3.2 Определение действующего значения токов цепи

Вычисляем токи ветвей и общий ток ветви:

;

;

;

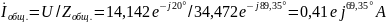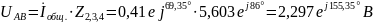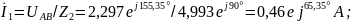
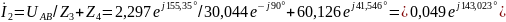
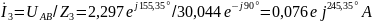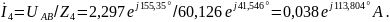
3.3 Составление уравнения мгновенного значения тока источника

Уравнение мгновенного значения тока источника:

;

.

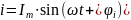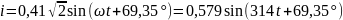3.4 Составление баланса активных и реактивных мощностей

Рассчитаем комплексную мощность цепи:

;

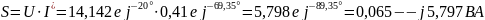где ;

;

.

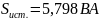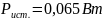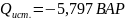Активная 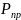и реактивная 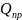мощности приёмников:

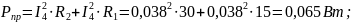
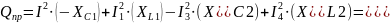
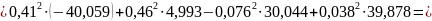
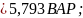
Определим напряжения на элементах схемы замещения:

;

;

;

;

;

.

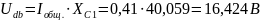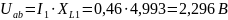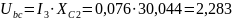
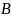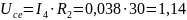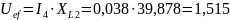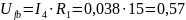3.5 Построение векторной диаграммы токов и напряжений

Строим топографическую векторную диаграмму на комплексной плоскости. Выбираем масштаб , .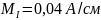

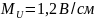Определяем длины векторов токов и напряжений:

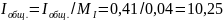см;

см;

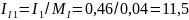см;

см;

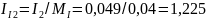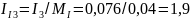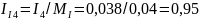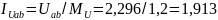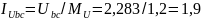см;

см;

см;

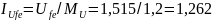см;

см;

см;

см.

На комплексной плоскости в масштабе откладываем векторы токов в соответствии с расчетными; значениями, при этом положительные фазовые углы отсчитываем от оси (+1) против часовой стрелки, а отрицательные — по часовой стрелке.

Топографическая векторная диаграмма напряжений характерна тем, что каждой точке диаграммы соответствует определенная точка электри­ческой цепи. Построение векторов напряжений ведем, соблюдая порядок расположения элементов цепи и ориентируя векторы напряжений относи­тельно векторов тока: на активном сопротивлении ток и напряжение сов­падают по фазе, на индуктивном элементе напряжение опережает ток на 90°, а на ёмкостном напряжение отстает от тока на 90°. Направление обхо­да участков цепи выбираем, как принято, противоположно положительно­му направлению токов.

Векторная диаграмма токов и напряжений представлена в Приложении В.

4 Решение трёхфазной линейной цепи электрической цепи переменного тока

4.1 Нахождение фазных токов

В цепи, изображенной на рисунке 4.1, потребители трёхфазного тока соединены звездой. Известно линейное напряжение 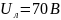и сопротивления фаз , , 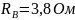, , 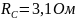, 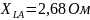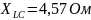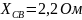. Определить полные сопротивления фаз, фазные токи и ток в ней­тральном проводе, активную, реактивную и полную мощности каждой фа­зы и всей цепи.

Дано:

; ;

; ;

; .

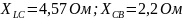Определить: .

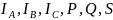При соединении треугольником 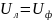=70. Так как есть нейтральный провод, то

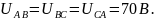
Выразим в комплексной форме фазные напряжения:

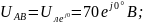
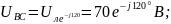
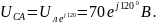
Выразим сопротивления фаз в комплексной форме:

.

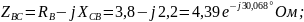
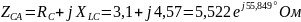Находим комплексы фазных токов

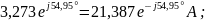
Модуль 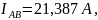аргумент

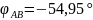
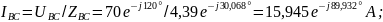
Модуль 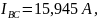аргумент .

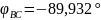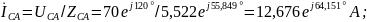
Модуль 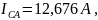аргумент .

Находим алгебраическую форму записи комплексов фазных токов: