Вопрос1.

Функции многих переменных. Частные производные функции многих переменных. Дифференциалы функции многих переменных.

Основные сведения из теории

Переменная величина z называется однозначной функцией двух переменных x и y, если каждой совокупности их значений (x, y) из данной области соответствует единственное значение z.

Переменные x,y называются аргументами или независимыми переменными. Функциональная зависимость обозначается так:

z=f(x,y), или z=F(x,y) (1)

Аналогично определяются функции трех и большего числа аргументов.

Под областью существования (определения) функции z=f(x,y) понимается совокупность точек (x,y) плоскости Oху, в которых данная функция определена, (т.е. принимает определенные действительные значения). В простейших случаях область существования функции представляет собой конечную или бесконечную часть координатной плоскости Oху, ограниченную одной или несколькими кривыми (граница области).

Линией уровня функции z = f (x,y) называется такая линия f (x,y)=c на плоскости Oху,, в точках которой функция принимает одно и тоже значение z=с.

Поверхностью уровня функции трех аргументов u=f(x,y,z) называется такая поверхность f (x,y,z)=c, в которых функция принимает постоянное значение с.

Пример 1.1. Найти область определения функции

Решение. Для того, чтобы квадратный корень имел вещественные значения, его подкоренное выражение должно быть неотрицательным. Решая неравенство (x-1)(y+2)≥0, находим, что

либо либо

Решением первой системы неравенств является x≥1, y≥ -2.

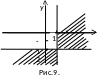
Решением второй - x≤1, y ≤ -2. Чтобы получить изображение искомой области на координатной плоскости, достаточно провести две прямые x=1 и y= -2. Полученные решения показывают, что область определения состоит из двух квадрантов с общей вершиной в точке (1,-2).

Пределы и непрерывность

Исследование пределов и непрерывности в многомерных пространствах приводит ко многим нелогичным и патологическим результатам, не свойственным функциям одной переменной. Например, существуют скалярные функции двух переменных, имеющих точки в области определения, которые при приближении вдоль произвольной прямой дают специфический предел, и дают другой предел при приближении вдоль параболы. Функция

стремится к нулю по любой прямой, проходящей через начало координат. Однако, когда к началу координат приближаются вдоль параболы  , предел = 0.5. Так как пределы по разным траекториям не совпадают, предела не существует.

Функция   имеет пределом число A при стремлении переменных  , соответственно, к  , если для каждого число   найдется такое число  , что  , то есть  .

Функция   называется непрерывной в точке  , если предельное значение этой функции в точке   существует и равно частному значению  .

Функция   называется непрерывной на множестве  , если она непрерывна в каждой точке этого множества.