47.Нахождение теоретической формы связи в корреляционном анализе.

При исследовании корреляционных связей между качественными признаками, представленными в виде альтернативных показателей, используют коэффициент ассоциации Юла (Ка) и коэффициент контингенции Пирсона (Кк).

Например:

Коэффициент ассоциации:

Ка = (а·d – b·c) ÷ (а·d + b·c).

В тех случаях, когда один из показателей отсутствует, величина коэффициента ассоциации будет равна 1, что дает неправильную оценку степени тесноты связи между признаками. В этом случае используют коэффициент контингенции:

Кк изменяется от –1 до +1, Кк < Ка всегда. Чем ближе коэффициент контингенции к единице, тем сильнее связь между факторным и результативным признаками.

ДА НЕТ

ДА а в

НЕТ с d ,

критерий адекватности математически функций в корреляци-м анализе. Критерий фишера.

Для оценки значимости индекса корреляции применяется F-критерий Фишера.

Где m – число параметров корреляционного уравнения.

Величина F_R – сравнивается с критическим значением F_K. Если F_R> F_K, то величина R признается существенной и синтезированная математическая модель может быть пригодной для практического использования.

.

в качестве критерия адекватности синтезируемых моделей использ-ся показатели минимальности сркдней ошибки аппроксимации.

, где уi-yxi линейное отклонение абсолютных велечин эмпирических и выравненых точек регрессии. Для прямой 21,6%, для полулогарифмической 25,2%

48.Проверка типичности параметров уравнения регрессии и значимости коэфициента и индекса корреляции.

Прежде чем использовать к-л модель в последующем анализе необходима проверка ее параметров на типичность

t-критерий стьюдента

-среднеквадратическое отклонение результативного признака от выравненного значения

-среднеквадратическое отклонение признака фактора от его сред-го знач-я

полученные значения ta0 ta1, сравниваются с tкритическим, кот получают по таблице, с учетом принятого уровня значимости альфа (5%ошибка) и числа степеней свободы к=n-m, n-число ед-ц совокупности, m-число параметров ,критерий Стьюдента должен быть больше tкритического

ta0>tr<ta1 , тогда параметры уравнения признаются типичными.

t-критерий Стьюдента для кэф-та корреляции

49.Множественная корреляция,

Множ-ая кррел-я- при которой производится анализ влияния на результативный признак двух или более признаков факторов.

Уравнение регрессии y=a0+a1x1+.....+anxm

Введем матричные обозначения

Х-матрица независ-х перемен-х(признак факора

=у

Матрица параметров =а

Уравнение регрессии в матричном виде

транспонированная матрица. Транспон-е-операция переноса строк исходной матрицы в положение столбцов

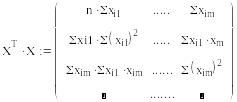
50. Непараметрические методы оценки корреляционной связи показателей.

Для определения тесноты связи, как между количественными, так и между качественными признаками используется коэффициенты Фехнера и Спирмена.

Коэффициент Фехнера вычисляется на основании определения знаков отклонения взаимосвязанных признаков x и y от их средних значений. Затем определяем число совпадений знаков отклонений для x и у, которое обозначается через а, а число несовпадений – через b, тогда коэффициент будет равен:

i = (Σa – Σb) ÷ (Σa + Σb) ,

чем ближе i к 1, тем связь теснее, чем i ближе к 0 - тем слабее.

Если значение признаков упорядочены (проранжированный) по степени убывания или возрастания признака, можно использовать для определения тесноты связи коэффициент рангов Спирмена:

р = 1 – (6 · Σdi²) ÷ (N · (N в квадрате – 1)) ,

где N – число наблюдений (число пар рангов)., di в квад-те—квадрат разости рангов связанных величинами х и у

Для определения d величины x и y сначала располагают в порядке увеличения, а затем производят ранжирование. Далее ранги записываются в соответствии с первоначальным расположением величин x и y и сравниваются между собой. Получают разность рангов величин x и y, равную d.