
- •1. Содержание предмета статистики. Задачи стат-ки.
- •2. Статистическая методология.Стат набл-е, сводка, анализ.
- •3.Статистич-е наблюдение, его сущность, задачи.
- •4. Программа наблюд-я, составные элементы.
- •5 Форма и виды наблюд-я
- •1. По характеру регистрации данных во времени:
- •6.Сплошные и не сплошные наблюдения. Способы организации наблюд-я.
- •7.Сводка материалов статис набл-я ,ее задачи и основное содержание.
- •8. Группировка-основа научной разработки материалов стат набл-я. Виды и основые задачи групп-к.
- •9. Классифик-я групп-х признаков.Основ-е правила образ-я групп по кол-ым признакам.
- •10.Статистические ряды распределения. Их виды. Графики рядов распределения.
- •11.Статистические таблицы, их виды .Простые(перечневые)табл. Групповые и комбинированные табл.
- •12.Основные правила составления таблиц
- •13. Графики, их значение и виды. Правила построения.
- •14. Виды статис-х величин: абсолют, относ, средние Абсолют-е величины их знач-я виды.
- •15. Относительные величины их виды и формы выражения.
- •16.Средние величины их сущность значение. Основные правила применения в ста-ке. Правило мажорности средних.
- •17.Средняя арифметическая (простая и взвешенная) Ее св-ва
- •18. Взвешенные средние
- •20.Понятие вариации. Показатели вариации размах вариации, среднее линейное отклонение
- •21.Свойства дисперсии,позвол-ие упростить расчеты. Показатели относительно рассеивания, коэф-т осцилляции, относит-е миним-ое отклонение, коэф-т вариации
- •3.Коэффициент вариации
- •22.Виды дисперсий, закон сложения дисперсий. Дисперсия альтернативного признака.
- •23 Понятие о выборочном наблюдении и его задачах. Генеральная и выборочная совокупность. Доля и средняя.
- •24.Понятие об ошибке выборки . Способы расчета средней ошибки выборки.
- •25 Предельная ошибка выборки. Расчет необходимой численности выборки
- •26.Способы образования выборочных совокупностей
- •27.Понятие о закономерности распределения. Тип распределения
- •30.Ряды динамики и их виды. Сопоставимость в рядах динамики.
- •31.Расчет среднего уровня в рядах динамики.
- •32. Показатели рядов динамики. Средние показатели в рядах динамики.
- •33.Сравнительный анализ рядов динамики одноименных велечин. Приведение рядов динам. К общему основанию.
- •34. Приемы обработки р.Д. (укрупнение интервалов, сглаживание методом скользящей средней)
- •37. ИнтерполяциЯ и экстрополяция в р.Д.
- •38. Изучение сезонных колебаний. Способы расчета Индекса сезонности.
- •39. Индексный метод в статистических исследованиях. Классификация индексов. Индивидуалдьные и общие индексы.
- •42. Индексы с постоянными и пременными весами
- •43.Индексный метод анализа факторов динамики. Изучения влияния структурных сдвигов с помощью индексов.
- •Iстр- индекс, отображающий влияние изменения структуры явления на изменение средней величины;
- •44.Территориальные индексы.
- •45.Виды взаимосвязей, изучаемы в статистике. Задачи корреляционного анализа.
- •46.Показатели тесноты корреляционной связи.
- •47.Нахождение теоретической формы связи в корреляционном анализе.
- •48.Проверка типичности параметров уравнения регрессии и значимости коэфициента и индекса корреляции.
- •50. Непараметрические методы оценки корреляционной связи показателей.
- •51 Секторно-отраслевая классиф-я.
- •52 Корпорация, органы гос-ого управления.
- •53 Домашнее хоз-во, некоммерче- ские учреждения (нку).
- •54 Территориальное расположение институциональных ед-ц (эк-ая территория, резидент).
- •55 Секторная структура рыночной эк-ки.
- •56 Международная стандартная отраслевая классификация (нсок) видов экономической деятельности.
- •58 Принцип построения национальных счетов. Матрично-аналитическое и граф-ое представление 4-х основных счетов.
- •59 Общая характеристика ввп и методы его исчисления.
- •2 Типа выпуска
- •61 Исчисление показателей ввп в постоянных ценах (методы).
- •62 Счёт образования дохода. Состав вдс.
- •63 Счёт первичного распределения дохода. Счёт вторичного распределения дохода.
- •64 Счёт использования располагаемого дохода.
- •67 Понятие национального богатства, балансы активов и пассивов.
- •68 Классификация национального богатства.
- •69 Классификация основных фондов. Методы оценки оф.
- •70 Методы исчисления амортизации.
- •71 Балансы основных фондов.
- •72 Показатели состояния, воспроизводства и использования основных фондов (оф).
45.Виды взаимосвязей, изучаемы в статистике. Задачи корреляционного анализа.
Статистические показатели могут состоять между собой в следующих основных видах связи: факторной, компонентной, балансовой.
В факторной связи показатели выступают как факторы, воздействующие на другие показатели или как результативные, испытывающие на себе влияние других.
Факторные связи могут рассматриваться как функциональные и корреляционные.
При функциональной связи изменение результативного признака y полностью зависит от изменения факторного признака x: y=f (x)- это связь жесткая. Знание функциональных зависимостей позволяет достаточно точно прогнозировать события.
При корреляционной связи значение результативного признака y частично зависит от факторного признака x, т.к. возможно влияние других факторов. Корреляционные связи- соотносительные-, неполные. В них одному значению признака- фактора может соответствовать несколько значений результативного признака.
Компонентные связи характеризуются тем, что изменение статистического показателя определяется изменением компонентов, входящих в этот показатель, как множители:
a=b∙c
Балансовая связь- показателей характеризует зависимость между источниками формирования ресурсов (средств) и их использованием описывается формулами вида:
a+b=c+d- баланс (равенство обеих частей).
При изучении корреляционной связи статистических показателей решаются следующие задачи:
Обнаружение зависимости между факторным и результативным признаками и установление формы связи
Установление силы (тесноты) связи, т.е. степени приближения ее к функциональной.
Первая задача решается соответствующей обработкой материала и выводом уравнения корреляционной связи, а вторая – расчетом специальных показателей тесноты связи.
Метод аналитических группировок служит для выявления корреляционной зависимости между отдельными признаками элементов совокупности. Для этого совокупность разбивают на группы по значению признака – фактора и в каждой группе определяют среднее значение результативного признака. Если с изменением признака-фактора закономерно меняется средняя величина результативного признака, то между ними есть связь. Для количественного измерения тесноты связи между факторным и результативным признаками находим коэффициент детерминации и корреляционное отношение.
Коэффициент детерминации:
![]()
2 – дисперсия групповых уровней,
2 – среднегрупповая дисперсия
![]()
![]() ,
,
_
где уср – групповые средние, у - общая средняя.
Коэффициент детерминации показывает насколько признак-фактор определяет результативный признак.
Корреляционное отношение
![]()
Корреляционное отношение показывает тесноту связи между исследуемыми признаками.если = 1, то связь функциональна, если = 0, то связь отсутствует, если 0 < < 1, то связь корреляционная.
46.Показатели тесноты корреляционной связи.
При прямолинейной связи показатель тесноты связи опр по формуле линейного коэф-та корреляции
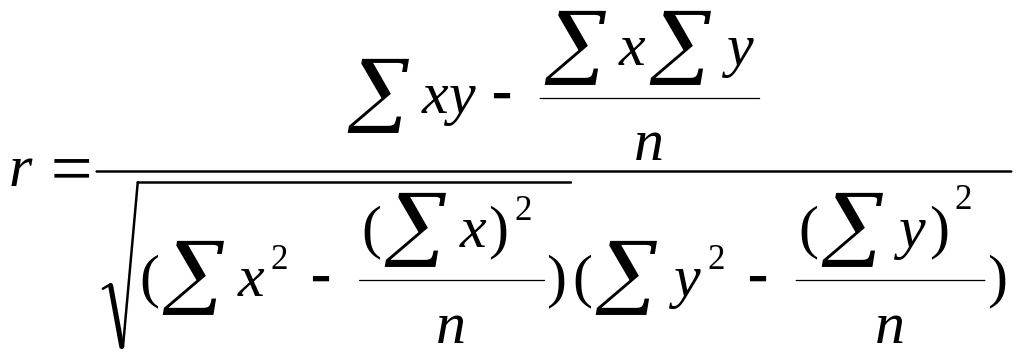
для получения вывода показателям тесноты связи дается качественная оценка по шкале Чедока.
0,1-0,3-слабая связь; 0,3-0,5-умеренная связь ; 0,5-0,7-заметная; 0,7-0,9- высокая ; 0,9-0,990-весьма высркая. Коэф-т кор-ции показывает и направление связи (-1 до1), если r>0, то прямая , r<0, то обратная
При полулогарифмич связи использся индекс детерминации и индекс корреляции
индекс детерминации
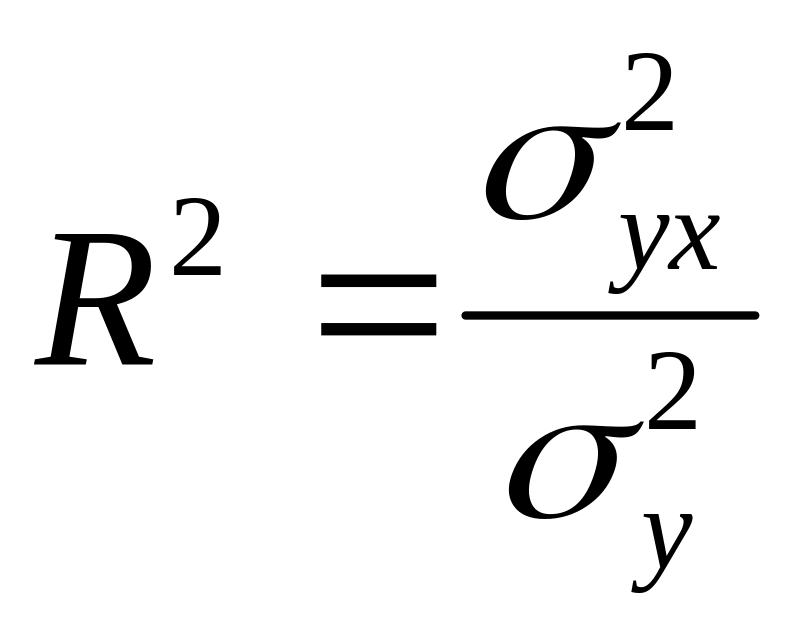
![]() -факторная
дисперсия , влияние изучаемого
признака-фактора на результативный
признак ;
-факторная
дисперсия , влияние изучаемого
признака-фактора на результативный
признак ;
![]() -общая
дисперсия, влияние всех факторов на
результативный признак
-общая
дисперсия, влияние всех факторов на
результативный признак
индекс корреляции
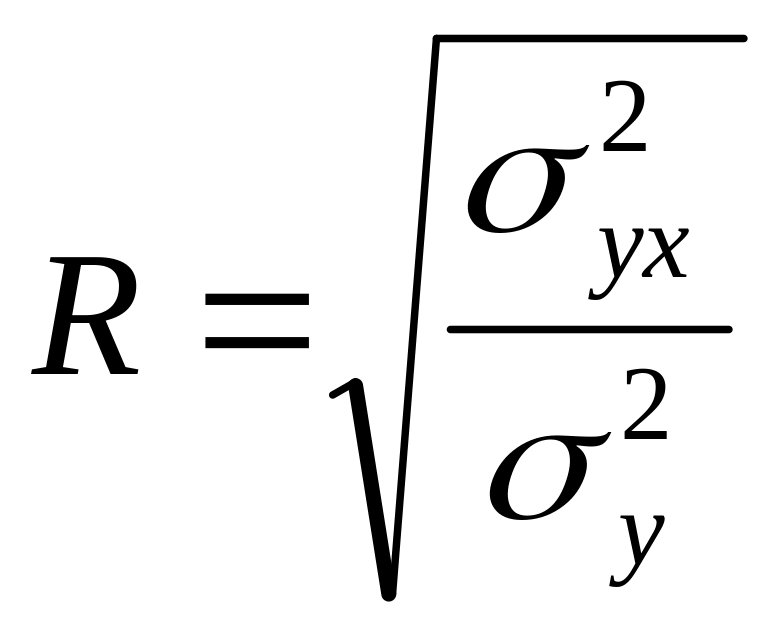
Если использовать правило сложения дисперсий
![]()

![]()
![]()
![]() остаточная
дисперсия, влияние всех остальных
факторов, кроме исследуемого не
результативный признак
остаточная
дисперсия, влияние всех остальных
факторов, кроме исследуемого не
результативный признак
