37. ИнтерполяциЯ и экстрополяция в р.Д.

Интерполяция – это определение значения недостающего члена ряда. Экстраполяция – это распространение выявленных в анализе рядов динамики закономерностей развития изучаемого явления на будущее. Чем скорее срок прогноза, тем надежнее результаты.

Применение методов экстраполяции зависит от характера изменений в ряду динамики.

1) при изучении рада динамики с постоянными абсолютными приростами - применяется формула: ;

где у_n+l – экстраполируемый уровень, , у_n – конечный уровень ряда.

2) при изучении ряда динамики со стабильными темпами роста

используется формула:

.3)Эксторополируемый уровень можнопределить используя трендовую модель

38. Изучение сезонных колебаний. Способы расчета Индекса сезонности.

Сезонные колебания – это более или менее устойчивые внутригодовые колебания уровней развития социально-экономических явлений.

При изучении внутригодовой динамики сезонных колебаний решают следующие задачи:

1 выявления специфики развития изучаемого явления.

2 изучение сезонных колебаний изучаемого явления с построением модели сезонной волны.

Для измерения сезонных колебаний используется индекс сезонности: isi = уi ÷ yti ,

где yi – исходные уровни ряда динамики, yti – теоретические (расчетные) уровни ряда динамики.

Чтобы исключить влияние случайных отклонений определяют средние индексы сезонности: isi = (Σ isi) ÷ n

В зависимости от характера тренда формула принимает следующие формулы:

Для рядов внутригодовой динамики с ярко выраженной основной тенденцией развития: _ isi = (Σ (уi /yti)) ÷ n

изменение сезон-х колеб-й на базе перемен-х уровней тренда наз способ переменной средней, где yti -теоретические уровни, выступающие в роли переменной базы.

Для рядов внутригодовой динамики, в которых повышающийся (понижающийся) тренд отсутствует или незначителен:

_ _ _

iх = уi ÷ y _

Так как y – общий средний уровень ряда выступает в роли постоянной базы сравнения, этот способ называется способом постоянной средней.

Вычисленные средние индексы сезонности составляют модель сезонной волны.

39. Индексный метод в статистических исследованиях. Классификация индексов. Индивидуалдьные и общие индексы.

Статистический индекс – это относительная величина сравнения двух совокупностей, элементы которых непосредственно не поддаются суммированию.

В зависимости от степени охвата единиц совокупности индексы подразделяются на индивидуальные и общие. В свою очередь общие индексы имеют две формы: агрегатную и среднюю.Основой индексного метода при определенных изменениях в производстве и обращении товара явл. переход от натуральновеществен-й фрмы выражения товарных масс к стоимостным измерителям.Индивидуальные индексы характеризуют изменения отдельных единиц совокупности. Общие индексы выражают сводные (обобщающие) результаты изменения всех единиц совокупности. Из общих выделяют групповые индексы выражающие изменения части единиц совокупности.

При изучении динамики исследуемых явлений сравниваемая величина принимается за текущий (отчетный) период, а величина, с которой производится сравнение – за базисный (плановый) период.Индексируемая величина – это величина, изменение которой можно установить при помощи индексов.

И ндивидуальные индексы физического объема реализации товаров

где q₁ и q₂ –количество продажи одного вида товаров в текущем и базисном периодах, в натуральных единицах.

И ндивидуальные индексы цен

где p₁ и p₀ – цены за единицу товара в текущем и базисном периодах

Общие индексы могут вычисляться по агрегатной и средней форме (средний арифметический и средний гармонический индексы). Выбор формы зависит от характера исходных данных. Например, агрегатный индекс цен

Агрегатный индекс физического объема товарной массы

Средний индекс цен

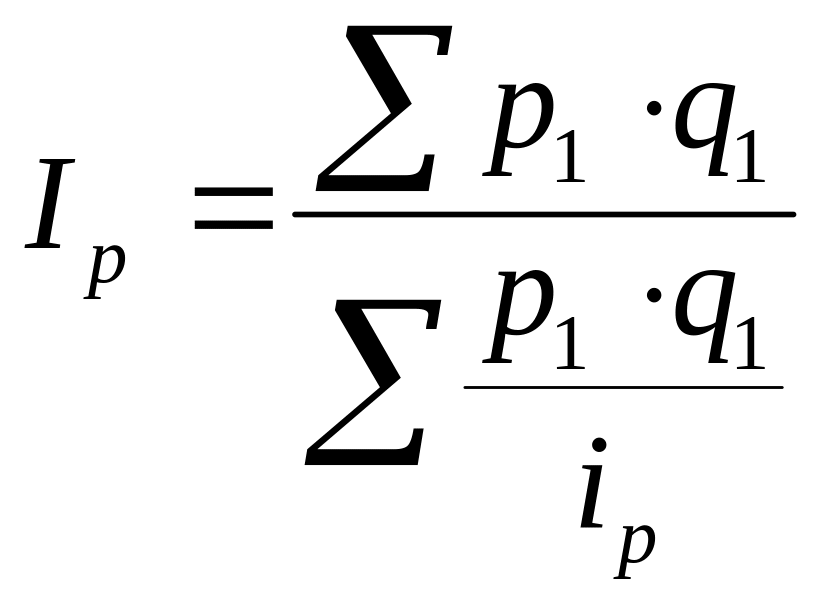
Средний индекс физического объема товарооборота или товаров

40-41. принципы построения агрегатных индексов. Преобразование агрегатного ин-декса в среднеарифметический индекс. Преобразование агрегатного индекса в среднегармонический индекс.

Основной формой общих индексов являются агрегатные индексы. В числитель и знаменатель общих индексов вводятся сомножители, называемые соизмерителями или весами. Они необходимы для перехода от натуральных измерителей разнородных единиц совокупности к однородным показателям. При этом в числителе и знаменателе общего индекса изменяется лишь значение индексируемой величины, а соизмерители являются постоянными величинами и фиксируются на одном уровне (текущего или базисного периода).

Агрегатный индекс цен (Пааше) образуется умножением числителя и знаменателя на q₁ – количество реализации товаров в текущем году

числитель-сумма стоимости продаж товаров в текущем периоде по ценам текущего преиода

знаменатель- сумма стоимости продаж товаров в текущем периоде по ценам базисного периода.

Данный индекс дает возможность определить изменение цен по данному ассортименту товаров. При сравнении числителя и знаменателя I_p определяется показатель абсолютного прироста товарооборота за счет фактора изменения цен в текущем периоде по сравнению с базисным

Если в качестве соизмерителя использовать q₀ – количество реализации товаров в базисном периоде, то получится агрегатный индекс Ласпейреса

числитель сумма стоимости продаж товаров в базисном периоде по ценам текущего периода

знаменатель- сумма стоимости продаж товаров в базисном периоде по ценам базисного периода. показатель абсолютного прироста товарооборота

Для определения агрегатного индекса физического объема товаров в качестве соизмерителей индексируемых величин q₁ и q₀ могу применяться неизмененные цены либо базисного, либо отчетного периода

изменениеV прдук-и в базисн-х ценах в текущих ценах

По данным формулам определяется изменение физического объема реализации товаров в текущем периоде по сравнению с базисным.

При сравнении числителя и знаменателя получаем показатель абсолютного прироста товарооборота. Например,

По данной формуле получаем прирост товарооборота в текущем периоде по сравнению с базовым в базисных ценах.

Баланс отклонения

Так как не всегда ведется учет продажа отдельных товаров ,то есть не известно q0, тто для определения сводных общих показателей изменения розничных цен использ-ся средняя гармонич. индекс. Проведем преобразование агрегатного индекса в средний

путем замены . Получаем среднегармонич-й индекс цен 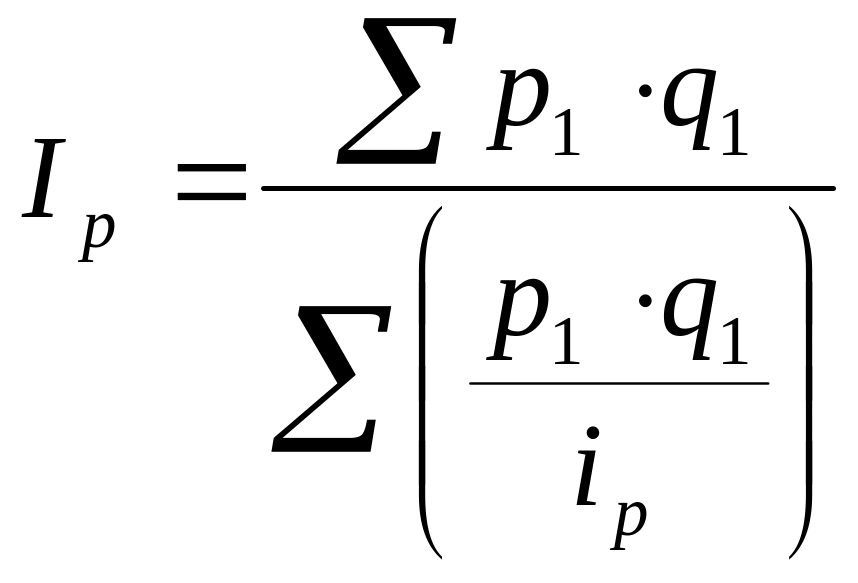где -товарооборот текущего периода в стоимостном выражении

Все индексы качественных показателей это средние гармонич-е величины

Средний арифметический индекс физического объема товарооборота получаем заменой в агрегатном индексе

.