4.3.1. Представление плоских кривых

В предыдущих подразделах изучались преобразования точек. Кривая может быть представлена совокупностью точек. Если точки расположены близко друг от друга, то, соединяя их отрезками прямой, можно получить изображение кривой. На рис. 4.19 показаны два разных точечных представления одной кривой. Точки на кривой рис. 4.19, а расположены равномерно по ее длине. В результате получается довольно плохое представление кривой, особенно, если мал радиус кривизны. Улучшить вид можно, увеличивая плотность точек в таких участках (рис. 4.19, б).

Хотя, как показано выше, кривые могут быть достаточно хорошо представлены совокупностью точек, аналитическое представление во многих отношениях предпочтительнее. Его преимущество – это точность, компактность записи и простота вычисления промежуточных точек. Аналитическое представление позволяет без труда определить наклон и радиус кривизны, а при точечном представлении для этого требуется численное дифференцирование – чрезвычайно неточная процедура. Сравните объем памяти для точечного представления окружности с 32 точками на ней и аналитическое представление – координаты центра и радиус. При аналитическом представлении кривой можно точно определить положение любой точки, а при точечном нужна интерполяция, причем в общем случае результат интерполяции не принадлежит кривой.

Опыт показывает, что аналитически представленные кривые легче изобразить на рисунке. Аналитическое представление выгоднее, когда для удовлетворения заданному критерию необходимо непрерывно изменять форму кривой. Ниже рассматриваются различные методы аналитического представления двумерных кривых.

Часто требуется аналитическое представление кривой, первоначально заданной точками. С математической точки зрения это проблема интерполяции. Для того чтобы провести кривую через все заданные точки, применяется метод кусочной полиномиальной аппроксимации. Для этого требуется определить коэффициенты полинома некоторой степени. Вид кривой в промежуточных точках зависит от степени полинома и граничных условий.

Если же точки – только приблизительные значения величин, например данные экспериментальных измерений или наблюдений, то нужна кривая, задающая верное направление изменения. В общем случае кривая может не проходить ни через одну точку данных. Здесь применяется метод наименьших квадратов. Метод наименьших квадратов дает кривую в виде y = f(x), которая минимизирует сумму квадратов отклонений по оси у между данными и полученной кривой. Вид y = f(x) выбирают исходя из характера изучаемого процесса.

Обычно для метода наименьших квадратов используются полиномы, степенные и экспоненциальные функции:

y = ax^b, y = ae^bx или y = c1+ c2x+c3x²+…+c_n+1 xⁿ,

где a, b и c_j – константы. Независимо от выбора вида кривой метод требует решения системы линейных алгебраических уравнений для определения неизвестных констант.

4.3.1.1. Непараметрические кривые

Математически кривая может быть представлена в параметрической или непараметрической форме. Непараметрическая кривая задается в виде явной или неявной функции. Для плоской кривой явное непараметрическое представление имеет вид:

.

Пример – уравнение прямой y = mx + b. При этом одному значению х соответствует только одно значение у, поэтому замкнутые или многозначные кривые, например окружность, явно представить нельзя. Неявное представление

,

позволяет обойти это ограничение. Общий вид неявного уравнения второй степени

порождает различные двумерные кривые, называемые коническими сечениями. На рис. 4.20 изображены три вида конических сечений – парабола, гипербола и эллипс. Окружность – это частный случай эллипса. Определяя коэффициенты а, b, c, d, e и f , можно получить разные конические сечения. Если сечение задано относительно локальной системы координат и проходит через ее начало, то f = 0. Для того чтобы провести кривую через данные точки, используются граничные условия.

Пусть с = 1,0, тогда сегмент кривой между точками определяется пятью независимыми условиями, из которых вычисляются оставшиеся коэффициенты a, b, d, e и f. Например, можно указать положение крайних точек, наклон кривой в них и промежуточную точку на кривой.

Если b = 0 и c =1,0, то аналитическое представление кривой получается с помощью только четырех дополнительных условий в них. Кривая при a = 1,0, b = 0 и c = 1,0 еще проще:

.

Тремя условиями для вычисления d, e и f могут быть две концевые точки и наклон кривой в одной из них или же две концевые точки и третья точка на кривой.

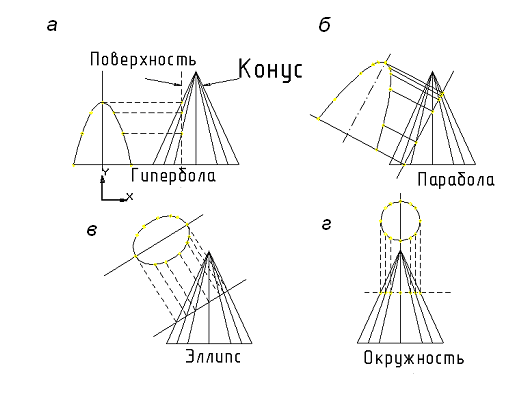
Рис. 4.20

При a = b = c = 0 получается прямая линия. Ее уравнение

или

где m – наклон линии; b’ – пересечение с осью у.

Как явное, так и неявное непараметрическое представление осезависимо, т. е. сложность обработки зависит от выбора системы координат. Например, если в заданной системе координат граничным условием является вертикальный наклон, нужно либо изменить ее, либо аппроксимировать бесконечный коэффициент наклона наибольшей допустимой положительной или отрицательной величиной.

Кроме того, если точки на осезависимой непараметрической кривой вычисляются с равномерным приращением по х или у, они не будут равномерно распределены вдоль кривой. Это может повлиять на качество и точность графического изображения. Тем не менее непараметрическое представление бывает полезным. Теперь рассмотрим параметрическое представление, позволяющее обойти эти ограничения.