
Сумма работ всех активных сил равнялась нулю на любом возможном перемещении, задаваемом из предполагаемого положения равновесия системы.
Доказательство:
F – внешние силы
R – силы реакции



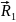
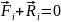
Просуммируем по всем точкам тела:
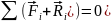
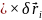
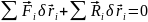
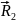 т.к.
т.к.
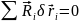 ,
то
,
то

ПРИНЦИП ВОЗМОЖНЫХ СКОРОСТЕЙ:
Для того, чтобы механическая система находилась в равновесии, необходимо и достаточно, чтобы возможная мощность всех активных сил на любых возможных скоростях была равна нулю.

ПРИНЦИП ЛАГРАНЖА ДЛЯ КОНСЕРВАТИВНОЙ МЕХАНИЧЕСКОЙ СИСТЕМЫ
В положении равновесия консервативной механической системы потенциальная энергия имеет стационарные значения.
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ:
 В
любой момент движения материальной
системы, находящейся под действием
активных сил, и на которую наложены
идеальные удерживающие стационарные
голономные связи, сумма работ активных
сил и сил инерции, действующих на все
точки системы на любом возможном
перемещении, равна нулю.
В
любой момент движения материальной
системы, находящейся под действием
активных сил, и на которую наложены
идеальные удерживающие стационарные
голономные связи, сумма работ активных
сил и сил инерции, действующих на все
точки системы на любом возможном
перемещении, равна нулю.
Доказательство:
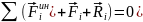

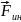
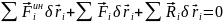
т.к.
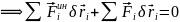
ОБОБЩЁННЫЕ КООРДИНАТЫ И ОБОБЩЁННЫЕ СИЛЫ
В аналитической механике декартовы координаты заменяются другими параметрами, имеющими любую размерность и геометрический (физический) смысл – углы, площади, дуги и т.п.
Независимые между собой параметры любой размерности, число которых равно числу степеней свободы системы и которые однозначно определяют её положение, называются обобщёнными координатами.
Обобщёнными силами называют такие величины, произведение которых на соответствующую обобщённую координату имеет размерность работы:
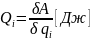
где Q – обобщённая сила, А – работа, qi – обобщённая координата.
- Если в системе движение невозможно, то у неё нет ни одной степени свободы
- Если возможно – мысленно фиксируем какую-либо одну меняющуюся координату. Если после этого движение стало невозможным – у системы 1 степень свободы.
- Если возможно – фиксируем вторую координату; и так до тех пор, пока тело не остановится.
ВЫРАЖЕНИЕ ОБЩЕГО УРАВНЕНИЯ ДИНАМИКИ В ОБОБЩЁННЫХ КООРДИНАТАХ:
Пусть имеется система, подчинённая голономным идеальным удерживающим связям и её положение в пространстве определяется координатами q1; q2 и т.д. Тогда общее уравнение динамики будет выглядеть следующим образом:
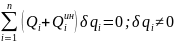
где Qi – обобщённая активная сила; Qiин – обобщённая сила инерции; δqi – обобщённая координата
УРАВНЕНИЕ ЛАГРАНЖА 2 РОДА
Число уравнений Лагранжа равно числу степеней свободы системы:
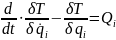
где Т – кинетическая
энергия системы в абсолютном движении;
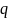 – обобщённая координата;
– обобщённая координата;
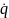 – обобщённая скорость; Qi
– обобщённая скорость по обобщённой
координате.
– обобщённая скорость; Qi
– обобщённая скорость по обобщённой
координате.
ЦИКЛИЧЕСКИЕ КООРДИНАТЫ.
Циклические координаты – это те обобщённые координаты, которые не входят ни в выражение кинетической энергии, ни в выражение потенциальной энергии.
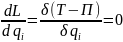
L – разность кинетической и потенциальной энергии.
Для циклической обобщённой координаты qi уравнение Лагранжа имеет следующий вид:
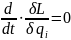
где
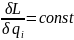 - циклический интеграл
- циклический интеграл
Аналитическая механика после Лагранжа получила большое развитие и применение в различных областях науки и техники; её методы особенно широко применяются в теории колебания систем и в квантовой механике.
