Вывод дифференциальных уравнений конвективного теплообмена Уравнение неразрывности.

Уравнение неразрывности мы будем выводить, используя локальный эйлеров подход. Будем использовать прозрачный для среды элемент постоянного объёма: .

^{П оток массы:} соответствующая площадь.

плотность потока массы

(*)

Изменение массы в выделенном объёме по времени зависит от потока массы через поверхность.

Это закон сохранения массы в выделенном объёме:

Преобразуем (*) по теореме Остроградского-Гаусса:

Поскольку V произвольно, то это равенство возможно только при равенстве подынтегральных выражений:

Это есть общее выражение закона сохранения массы или уравнение неразрывности.

Частный случай:

Несжимаемая среда .

пусть имеется плоское течение:

Уравнение сохранения количества движения

Рассмотрим субстанциональный подход, то есть около рассматриваемой точки мы исследуем макротело постоянной массы.

^{- обобщённый закон Ньютона.}

^{- главный вектор количества движения:}

В итоге получаем общее уравнение сохранения количества движения:

Уравнение сохранения количества движения не может быть математически раскрыто, так как состоит из трёх уравнений, и мы должны перейти к проекциям.

Проекция на ось Х:

- производная особого рода.

Преобразуем , используя гипотезу Ньютона-Стокса по связи тензора напряжений и тензора деформаций:

- учёт вязкости среды.

- учёт давления перемещения частиц в соответствующем поле сил.

Проекция на ось Х:

Совокупность уравнений, выражающих проекции на оси Х,У,Z, называются уравнениями Навье-Стокса.

Уравнение энергии

Используем субстанциональный подход.

Обозначим: Е – совокупность внутренней и кинетической энергии тела:

Составляющую энергии потенциальную мы выделим отдельно как работу массовых сил: I II

^{тепло + работа}

Разделим тепло внутренних источников и тепло, которое передаётся теплопроводностью или движением среды:

- тепло внутренних источников.

I _{по Остроградскому}

II: Выделим работу массовых сил и поверхностных сил:

работа массовых сил:

работа поверхностных сил:

^{заменим на , получим:}

^(а)

Домножим уравнение сохранения количества движения на вектор скорости:

(б)

^{Учитывая (б), из (а) получаем:}

Это общий вид уравнения энергии.

Преобразуем , используя гипотезу Ньютона-Стокса:

- работа сил вязкости (работа касательных напряжений).

Обобщённый вид:

- работа сил сжатия (расширения) среды.

и на порядки больше чем , и на 3-4 порядка больше .

Другая форма уравнения энергии.

Если мы сделаем замену: , мы получим:

(*)

Если среда жидкая, то (*) можно пренебречь для высокоскоростных потоков.

Запишем ещё один вариант – через энтропию:

Упрощённое представление: если мы представим и пренебрежём (*), получим:

Для безнапорных течений можно пренебречь , по Фурье , и если нет внутренних источников тепла, тогда:

и если , получим:

Однако такая запись уравнений не является общепринятой.

Итак, любое описание явления с помощью дифференциальных уравнений преобразуется к описанию обобщённого случая, если выразить математическое описание в относительных (безразмерных) величинах. При таком переходе обязательно получаются безразмерные комплексы.

Вся группа явлений описываемых обобщающим уравнением называется группой подобных явлений. Физики говорят, что явления этой группы можно рассматривать, как одно явление, данное в разных масштабах. Математики говорят, что тождество в относительном математическом представлении есть подобие в абсолютных величинах. Безразмерные отношения, входящие в описание подобных явлений называются критериями подобия. Первичные величины – это величины, характеризующие какое либо явление непосредственно без связи с другими величинами. Первичные величины могут быть получены прямым измерением и никогда не могут быть получены друг из друга. Пример первичной величины – время, координата… Любая вторичная величина определяется косвенным путём по численному значению первичных величин. В любом дифференциальном уравнении и условиях однозначности к этому уравнению имеются первичные величины и вторичные величины. Иногда вторичные величины называют искомыми величинами (например: скорость, температура, давление…). Кроме разделения на первичные и вторичные величины, принято выделять постоянные величины: . Следует обратить внимание, что эти постоянные величины являются постоянными только для конкретной задачи. Теперь на примере двух безразмерных комплексов и мы определим правильную технологию безразмерного комплекса. Если безразмерный комплекс составлен таким образом, что в него входит переменная величина, (например время), то такой комплекс называется число (число Фурье). Если для данной задачи все величины постоянны, то комплекс называется критерием подобия. const const

const

Введём безразмерные величины:

б езразмерная скорость

на удалении от стенки

^{Отнормируем:}

1. Возьмём уравнение неразрывности:

2. У равнение сохранения количества движения в проекции на ось Х

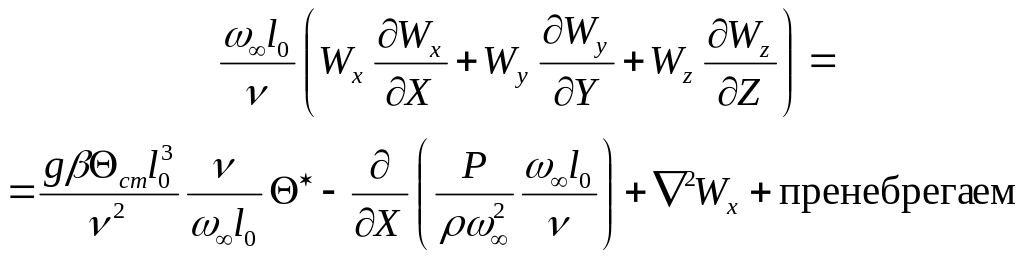
3. Уравнение энергии:

Примечание: кружочком выделены безразмерные величины.

Запишем граничные условия третьего рода:

Критерий Нуссельта:

Nu – безразмерный коэффициент теплоотдачи. Физически характеризует интенсивность теплообмена на границе «стенка – жидкость».

Замечание: Нуссельт по виду записывается как БИО, но не имеет никакого отношения к этому числу. Критерий Нуссельта относится только к жидкой среде.

Критерий Пекле:

характеризует соотношение количеств тепла, переносимого конвекцией и теплопроводностью.

- константы для задач.

Критерий Рейнольдса:

характеризует соотношение сил инерции и сил вязкости.

При малых числах Рейнольдса, выражено преобладание сил трения. Любое возмущение потока локализуется (гасится). Такое течение потока называется ламинарным (от латинского – «полоса»). При больших числах Рейнольдса (Re>2320) течение становится неустойчивым, возникает переходный режим. А при значительно больших значениях Рейнольдса возникает турбулентное течение (от латинского – «возмущающий»), появляются хаотические макропереносы массы и энергии. Механизм переноса массы, энергии и количества тепла при ламинарном течении – молекулярный. (Молекулярный перенос массы – диффузия.) Основной перенос массы, количества тепла и энергии в турбулентном потоке – макромеханизм (молярный).

Критерий Прандтля:

Рассмотрим уравнение количества движения и уравнение энергии:

Если рассматривать безнапорное движение, а влияние массовых сил будем считать малым, тогда у нас останется следующее:

характеризует соответствие поля скорости и поля температур (или характеризует степень подобия полей скорости и температур).

Если , то поле скорости и поле температур подобны для данной задачи.

Критерий Эйлера:

характеризует соотношение сил давления и сил инерции.

^{Его ещё записывают так:}

, где - давление окружающей среды.

Критерий Грасгофа:

характеризует подъёмную силу, возникающую вследствие разности плотностей.

Критерий Архимеда:

- для двух компонентных сред (вода с пузырьками).

^{- критерий Галилея.}

Критерий Фруда:

характеризует соотношение сил инерции и сил тяжести.