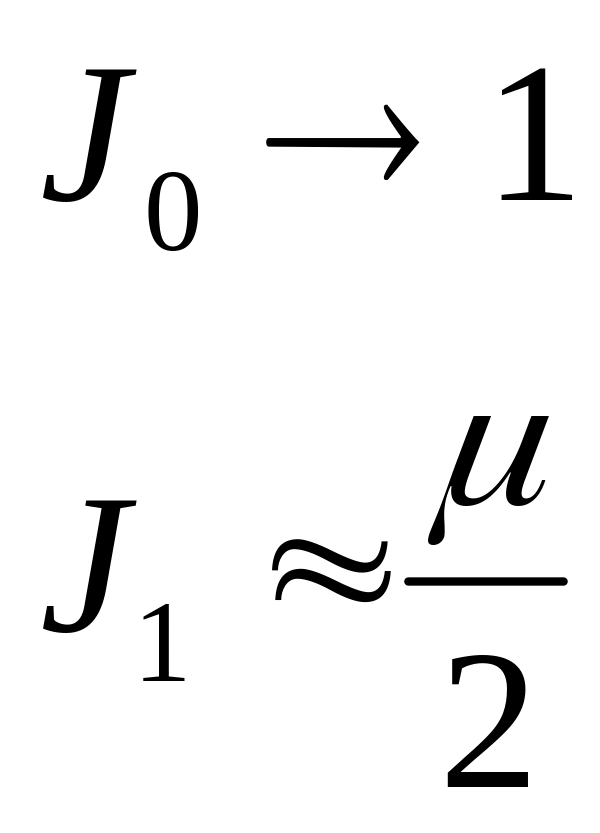- •Тепломассообмен
- •Теория тепломассообмена
- •Терминология. Общее представление о передачи тепла.
- •Феноменологический
- •Кинетический подход.
- •Если мы возьмём конвективный теплообмен между двумя средами, разделёнными твёрдой перегородкой, то процесс передачи тепла от горячей среды к холодной называется теплопередачей.
- •Фундаментальные соотношения, используемые в качестве замыкающих соотношений в теории тепломассообмена.
- •4) Гипотеза излучения
- •Вывод уравнения теплопроводности.
- •Классическое Уравнение Лапласа
- •Условия однозначности.
- •Решение стационарных задач теплопроводности. Температурное поле и тепловые потоки в плоской стенке
- •В бесконечной плоской стенке поле температур меняется в одном направлении – задача одномерная:
- •Значения температур
- •Температурное поле и плотность теплового потока в цилиндрической стенке.
- •Температурное поле и плотность теплового потока в шаровой (сферической) стенке.
- •Решение задач теплопроводности для граничных условий третьего рода. Плоская стенка. Теплопередача.
- •Вследствие того, что и , отсюда
- •Цилиндрическая стенка. Теплопередача.
- •Температурное поле в пластине (бесконечной плоской стенке) с внутренними источниками тепла.
- •Температурное поле в круговом цилиндре с внутренними источниками тепла.
- •Температурное поле цилиндрической стенки с внутренними источниками тепла.
- •Критический диаметр цилиндрической стенки. Выбор тепловой изоляции.
- •Выбор тепловой изоляции.
- •Интенсификация теплопередачи. В каком-то теплообменном аппарате через единицу поверхности передать наибольшее количество тепла.
- •Повышение интенсивности теплопередачи за счёт оребрения. Теплопроводность стержня (ребра постоянного поперечного сечения).
- •Обозначим:
- •Определение количества тепла, отводимого стержнем конечной длины в окружающую среду.
- •Теплопередача через ребристую плоскую стенку.
- •Коэффициент оребрения:
- •Круглое ребро постоянной толщины. Теплоотвод от круглого ребра.
- •Нестационарные процессы теплопроводности.
- •Охлаждение (нагревание) бесконечной пластины.
- •Задача одномерная, пусть
- •Обозначим:
- •Разложение функции в ряд Фурье
- •В таблицах и монограммах рассчитано для двух точек (в середине пластины
- •Случаи вырождения чисел био.
- •Охлаждение (нагревание) бесконечного цилиндра.
- •Почти уравнение Бесселя
- •Функция является производной
- •Анализ решения.
- •(Порядок малости)
- •Охлаждение (нагревание) тел конечных размеров.
- •Параллелепипед:
- •Цилиндр конечных размеров:
- •Определение количества тепла, отдаваемого телами при охлаждении.
- •Бесконечная пластина:
- •Бесконечный цилиндр:
- •Смотри справочные данные. Поиск сводится к средней температуре. Регулярный режим охлаждения (нагревания) тел.
- •Эта стадия охлаждения или нагревания когда описывается одним членом ряда называется регулярным режим охлаждения, нагревания тел.
- •Теоремы Кондратьева для регулярного режима.
- •Конвективный теплообмен.
- •Пути решения задач
- •Вывод дифференциальных уравнений конвективного теплообмена Уравнение неразрывности.
- •Уравнение сохранения количества движения
- •Уравнение энергии
- •Использование методов анализа размерности в задачах тепломассообмена.
- •Пример использования -теоремы.
- •Теорема Гухмана о подобных явлениях.
- •Система уравнений в приближения пограничного слоя.
- •Расчёт теплоотдачи при продольном обтекании пластины.
- •Результаты численного решения.
- •Решение задачи теплообмена на пластине.
- •Теплообмен при продольном обтекании пластины и турбулентном режиме течения. Аналогия Рейнольдса.
- •Расчёт интенсивности теплообмена при вынужденном стабилизированном течении жидкости в трубе. Особенности движения жидкости на начальном участке.
- •Принципиальные приближения:
- •Профили скорости при стабилизированном течении жидкости в трубе.
- •Расчёт интенсивности теплообмена при турбулентном течении жидкости в трубе.
- •Расчёт интенсивности теплообмена в шероховатых трубах.
- •Каналы некруглого поперечного сечения.
- •Изогнутые трубы (змеевики).
- •Кольцевые каналы.
- •Расчёт интенсивности теплообмена при поперечном обтекании трубного пучка.
В таблицах и монограммах рассчитано для двух точек (в середине пластины
Х=0 и на поверхности Х=1)


![]()



![]()
![]()
![]()

![]()
Одна монограмма для Х=0, другая – для Х=1
Случаи вырождения чисел био.
Вырождение – достижение некоторых предельных значений. Предельными значениями БИО являются бесконечно большие и бесконечно малые.
Бесконечно большое числоBi:
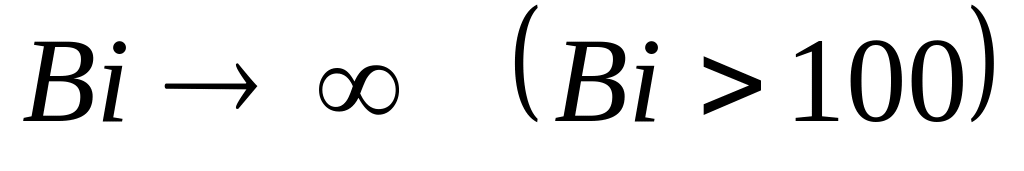 .
.
можно применять предельный подход:
при
![]() :
:
![]()
Если мы рассмотрим выражение для :
![]() причём:
причём:
![]()
так
как
![]() ,
то
,
то
![]()
Изобразим это:

![]()




![]()


![]()
![]()
![]()
Если поместить пластину в печь, то температура на её поверхности сразу станет равной температуре печи.
Если
![]() ,
мы получим:
,
мы получим:
![]() -
температура
на оси при больших временах.
-
температура
на оси при больших временах.
Выражая
![]() через
через
![]() ,
мы получим:
,
мы получим:
![]()
Это время достижения заданной температуры в центре пластины.
Бесконечно малое Био:

На
практике Био вырождено, если
![]()
Корни характеристического уравнения:
![]()
При
этом:
![]()
Для тонких тел температура описывается одним членом ряда независимо от числа .
![]()
Определим
порядок
![]() при
:
при
:
![]()

![]()
![]()
Поэтому для малых Био поле температур описывается одним единственным членом ряда:
![]()
Изобразим эту зависимость:

![]()
![]()

![]()
Это означает, что разница температур в центре и на поверхности стремится к нулю.
Рассмотрим
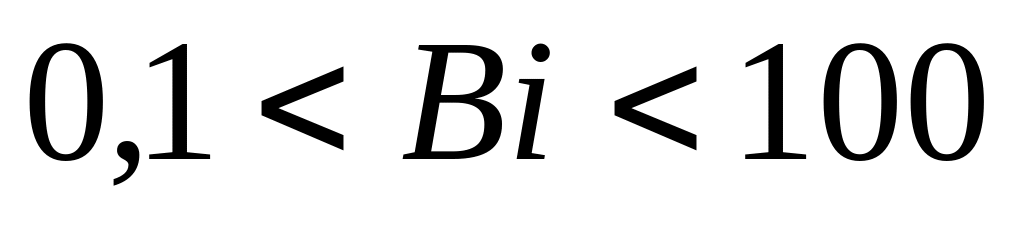 :
:

![]()
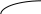
![]()






![]()
Охлаждение (нагревание) бесконечного цилиндра.
Рассмотрим
бесконечный цилиндр радиусом
![]() .
.
Известен
материал,
,
![]() .
Цилиндр размещён в среде с постоянной
.
Цилиндр размещён в среде с постоянной
![]() ,
коэффициент теплоотдачи
.
,
коэффициент теплоотдачи
.

![]()
Н ачальная
температура в любой точке цилиндра
ачальная
температура в любой точке цилиндра
![]()
Задача является одномерной.
![]()
решением является:
![]()
![]()
![]()


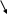
![]()
![]()
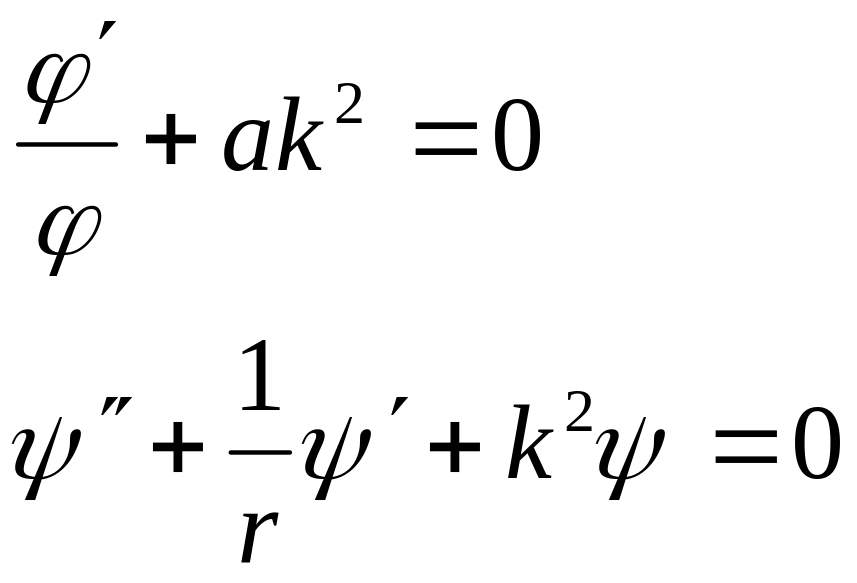

Почти уравнение Бесселя
его
решениями являются функции Бесселя
![]()
![]() -
функция Бесселя первого рода нулевого
порядка;
-
функция Бесселя первого рода нулевого
порядка;
![]() -
функция Бесселя первого рода первого
порядка.
-
функция Бесселя первого рода первого
порядка.
Начальные
условия:
![]()
Граничные условия:
1)
![]() -
условие
симметрии.
-
условие
симметрии.
2)
![]()
Общий вид решения:
![]()

![]() -
безразмерный радиус.
-
безразмерный радиус.
![]()
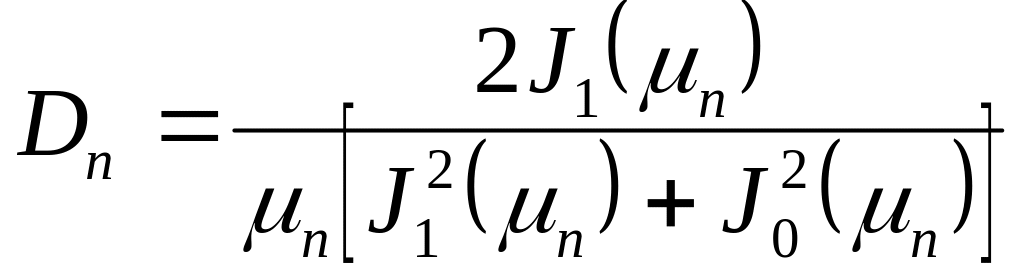
J0
– аналогично
![]()
J1
–
аналогично
![]()

![]()
![]()
![]()
Функция является производной
 1
1
![]()


2 4 6 8 10
-0,4
![]() -
бесконечные периодические функции с
уменьшающейся амплитудой.
-
бесконечные периодические функции с
уменьшающейся амплитудой.
![]()
 (*)
(*)
Характеристическое уравнение для расчёта корней.




![]()


![]()
![]()
![]()
![]()
![]()
![]()
Анализ решения.
Поскольку
временная функция такая же как и в
предыдущей задаче для
![]() ,
температурное поле описывается так же
одним членом ряда.
,
температурное поле описывается так же
одним членом ряда.
![]()



![]()

![]()
Поверхностный слой цилиндра мгновенно принимает температуру окружающей среды.
(Порядок малости)

подставим в (*), получим:
![]()
Рассчитаем при :
![]()
При вне зависимости от Фурье решение описывается первым членом ряда:
![]()
![]()
Изобразим температурное поле при :


0 1