Билет №6
Вопрос 1.
Нормальное распределение, также называемое гауссовым распределением или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:
где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1. Свойства:
Если случайные
величины
и
независимы
и имеют нормальное распределение с
математическими ожиданиями
и
и
дисперсиями
и
соответственно,
то
также
имеет нормальное распределение с
математическим ожиданием
и
дисперсией
.
Распределе́ние
Берну́лли
моделирует случайный
эксперимент
произвольной природы, когда заранее
известна вероятность
успеха или неудачи. Случайная
величина
имеет
распределение
Бернулли, если она принимает всего два
значения:
и
с
вероятностями
и
соответственно.
Таким образом:
,
.
Принято говорить,
что событие
соответствует
«успеху», а
«неудаче».
Эти названия условные, и в зависимости
от конкретной задачи могут быть заменены
на противоположные.
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
Распределение Пуассона играет ключевую роль в теории массового обслуживания.
Выберем
фиксированное число
и
определим дискретное
распределение,
задаваемое следующей функцией
вероятности:
,
где
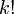обозначает
факториал,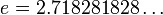
—
основание
натурального логарифма.
Свойства распределения Пуассона:
Сумма независимых пуассоновских случайных величин также имеет распределение Пуассона. Пусть
.
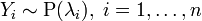Тогда
.
Пусть
,
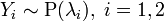и
.
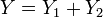Тогда условное
распределение
при
условии, что
,
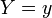биномиально. Более точно:
.
Математи́ческое ожида́ние — среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.
Пусть
задано вероятностное
пространство
и
определённая на нём случайная
величина
.
То есть, по определению,
—
измеримая
функция.
Если существует интеграл
Лебега
от
по
пространству
,
то он называется математическим
ожиданием, или средним (ожидаемым)
значением и обозначается
или
.
Примеры: Пусть
случайная величина имеет дискретное
равномерное распределение,
то есть
Тогда
её математическое ожидание
равно среднему арифметическому всех принимаемых значений.
Пусть случайная
величина имеет непрерывное
равномерное распределение
на интервале
,
где
.
Тогда её плотность имеет вид
и
математическое ожидание равно
.
Пусть случайная величина имеет стандартное распределение Коши. Тогда
,
то есть математическое ожидание не определено.
Диспе́рсия
случа́йной величины́ —
мера разброса данной случайной
величины,
то есть её отклонения от математического
ожидания.
Обозначается
в
русской литературе и
(англ. variance)
в зарубежной. В статистике часто
употребляется обозначение
или
.
Квадратный корень из дисперсии, равный
,
называется среднеквадрати́чным
отклоне́нием,
станда́ртным
отклоне́нием
или стандартным разбросом. Стандартное
отклонение измеряется в тех же единицах,
что и сама случайная величина, а дисперсия
измеряется в квадратах этой единицы
измерения. Пусть
—
случайная величина, определённая на
некотором вероятностном
пространстве. Тогда
где символ
обозначает
математическое
ожидание