Министерство образования Российской Федерации

Уфимский Государственный Авиационный Технический Университет

Кафедра АТС

Расчётно-графическая работа

по дисциплине

«Диагностика и надежность технических систем»

на тему

«Расчет и повышение надежности

технической системы»

ВАРИАНТ 6

Выполнил: студент гр. АТП-422

Проверил: Никитин Ю.А.

Уфа, 2006 г

ЗАДАНИЕ

По структурной схеме надежности технической системы в соответствии с вариантом задания , требуемому значению вероятности безотказной работы системы γ и значениям интенсивностей отказов ее элементов γ , требуется:

1. Построить график изменения вероятности безотказной работы системы от времени наработки в диапазоне снижения вероятности до уровня 0.1-0.2.

2. Определить γ-процентную наработку технической системы.

3. Обеспечить увеличение γ-процентной наработки не менее ,чем в 1,5 раза за счет :

А) повышения надежности элементов;

В) структурного резервирования элементов системы.

Все элементы системы работают в режиме нормальной эксплуатации (простейший поток отказов) Резервирование отдельных элементов или групп элементов осуществляется идентичными по надежности резервными элементами или группами элементов .Переключатели при резервировании считаются идеальными.

На схемах обведенные пунктиром m элементов являются функционально необходимыми из n параллельных ветвей.

γ%= 75

λ₁= 0.01×10^-6

λ_2-11= 1×10^-6

λ_{12, 13}= 0.05×10^-6

λ₁₄= 0.1×10^-6

Декомпозиция схемы

Рис.1 Исходная система

1. В исходной схеме элементы: 4, 5 образуют последовательное соединение. Заменяем их элементом А. Учитывая ,что p₄=p₅ получим:

p_A=p₄p₅ = p₄²

2. Элементы: 6, 7 образуют последовательное соединение. Заменяем их элементом B. Учитывая ,что p₆=p₇ получим:

p_B=p₆p₇ = p₆²

4. Элементы: 8, 9 образуют последовательное соединение. Заменяем их элементом C. Учитывая ,что p₈=p₉ получим:

p_C=p₈p₉ = p₈²

5. Элементы: 10, 11 образуют последовательное соединение. Заменяем их элементом D. Учитывая ,что p₁₀=p₁₁ получим:

p_D=p₁₀p₁₁ = p₁₀²

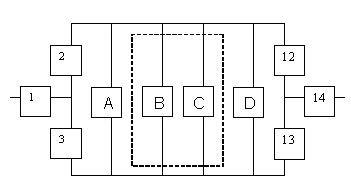
Рис. 2 Преобразованная система

4. Элементы A, B, C, D образуют систему типа “m из n”. Заменяем их элементом E.

Рис. 3

Для мостиковой схемы (рис. 3) в качестве особого элемента целесообразно выбрать диагональный элемент E. При р_E =1 мостиковая схема превращается в параллельно-последовательное соединение, а при р_E =0 – в последовательно-параллельное

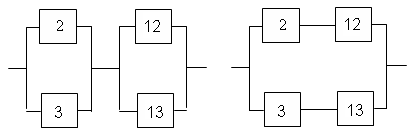
Рис. 4 Преобразование мостиковой схемы

при абсолютно надежном (а) и отказавшем (б) центральном элементе.

Для преобразованных схем можно записать:

Рис. 5

На этом этапе считаем декомпозицию схемы законченной (осталось всего 3 последовательно соединенных элемента).

Определение γ-процентной наработки т с.

Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с 1 по 15 подчиняются экспоненциальному закону :

exp(-). (1)

Результаты расчетов вероятностей безотказной работы элементов 1-14 ис­ходной схемы по формуле (1) представлены в таблице 1.

Результаты расчетов- вероятностей безотказной работы квазиэлементов А, В, С,D, Е, F и G по найденным в п.1 формулам также представлены в таблице 1.

На рис. 1 представлен график зависимости вероятности безотказной работы системы Р от времени (наработки) t.

По графику (рис. 1, кривая Р) находим для γ= 75% (Р = 0.75) γ- процентную наработку системы Т_γ =0.58 ×10 ч.

Проверочный расчет при t= 0.58×10 ч показывает (таблица 1), что P_γ =0.74721≈ 0.75

Обеспечение увеличения γ-процентной наработки не менее ,чем в 1,5 раза за счет повышения надежности элементов.

По условиям задания повышенная γ - процентная наработка системы

=1.5T. = 1,5•0,58•10 = 0.87×10 ч.

Расчет показывает (таблица 1), что при t =0.87×10⁶ ч для элементов преобразованной схемы (рис. 5) p₁=0.9913, p_G = 0.6441, p₁₄= 0.9167. Следовательно, из трех последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет элемент G и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.

Для того, чтобы при = 0.87×10⁶ ч система в целом имела вероятность безотказной работы Р_g =0.75, необходимо, чтобы элемент G имел вероятность безотказной работы .

При этом значении элемент G останется самым ненадежным в схеме.

Однако, т.к. аналитическое выражение этого уравнения связано с определенными трудностями, более целесообразно использовать графоаналитический метод. для этого строим график зависимости P_G =f (p₁₂).

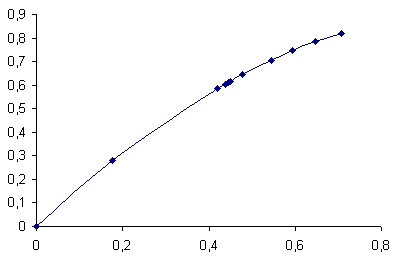
По графику при p_G = 0.837 находим p₁₂»0,7375

Тогда λ_2-11’==0,35×10⁶

Результаты расчетов для системы с увеличенной надежностью элементов 2- 11 приведены в таблице 1