6. Определение нормальных напряжений в поперечном сечении в общем случае сложного сопротивления.

В общем случае пространственного действия сил на стержень внутренние усилия в поперечном сечении приводятся к шести компонентам: продольному усилию N_z, крутящему моменту М_к, поперечным силам Q_х, Q_у и изгибающим моментам М_х, М_у. Если ось z – геометрическая ось стержня, а оси х и у – главные центральные оси инерции поперечного сечения, центр тяжести которого совпадает с центром изгиба, то Q_у и М_х определяют собой поперечный изгиб в плоскости xz, а Q_х и М_у – поперечный изгиб в плоскости yz. Таким образом, стержень испытывает одновременную деформацию растяжения или сжатия, кручения и двух прямых поперечных изгибов.

Отрезки, отсекаемые нулевой линией п–п на осях координат, определяются по формулам:

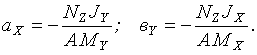                               (13) 

Моменты М_х и М_у принимаются со знаком «+», если они растягивают точки сечения в первой четверти осей координат х, у.

Угол β между плоскостью действия результирующего момента  (силовой плоскостью F–F) и вертикальной плоскостью yz найдется из выражения

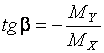                                            .                                            (14) 

В произвольной точке (х, у) поперечного сечения стержня нормальное напряжение определяются по формуле (7)

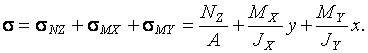
Результирующее касательное напряжение находим путем геометрического сложения касательных напряжений от кручения и изгиба. Касательные напряжения от изгиба обычно невелики. Тогда учитываются только касательные напряжения от крутящего момента, которые определяются по формулам:

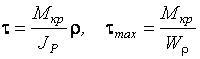,                                      (15)

 

где  – полярный момент инерции сечения; ρ – расстояние от центра тяжести сечения до рассматриваемой точки;  – полярный момент сопротивления сечения. 

7. Формула Верещагина для определения перемещений и условие жесткости.

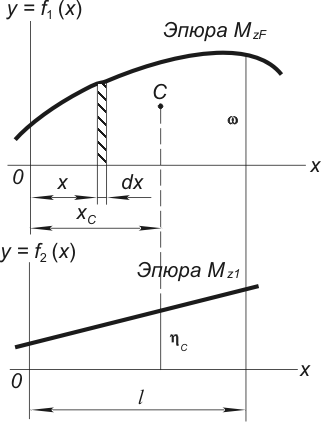
Вычисление интеграла Мора целесообразно вести по правилу, предложенному А. Н. Верещагиным в 1925 г. для прямолинейных брусьев. Уравнения изгибающих моментов и , входящие в формулу интеграла Мора, - это некоторые функции от х: , , а графики этих функций - эпюры и (рисунок 1) на некотором участке балки. Причем если первая функция может быть и нелинейной, то вторая , выражающая изгибающий момент от единичной силы (или единичного момента), обязательно линейная. Поэтому ее можно представить уравнением прямой с угловым коэффициентом, т. е. . Следовательно, вычисление интеграла можно заменить вычислением интеграла . Раскрыв скобки под интегралом в правой части равенства, получим

Рисунок 1

П роизведение есть не что иное, как заштрихованная на рисунке 1 элементарная площадка эпюры . Значит, первый интеграл в правой части равенства выражает площадь эпюры в интервале от х=0 до x=l, а второй интеграл - статический момент этой же площади относительно оси у, который, как известно из формулы, выражается произведением площади на координату ее центра тяжести С. Если площадь эпюры обозначить буквой , то равенство примет вид

, где , т. е. ордината эпюры под центром тяжести С эпюры . Следовательно, в окончательном виде . Теперь формула интеграла Мора может быть записана так:

.

Таким образом, правило Верещагина состоит в том, что интеграл Мора, составленный для каждого из участков нагружения балки, равен произведению площади нелинейной эпюры изгибающих моментов на ординату эпюры изгибающего момента , соответствующую положению центра тяжести площади . Вычисление интеграла Мора по правилу Верещагина обычно называют методом перемножения эпюр. Эпюра называется грузовой эпюрой, а эпюра - единичной. При перемножении эпюр необходимо иметь в виду следующее: произведение , если площадь и ордината расположены по одну сторону от базовых линий; при расположении и по разные стороны от базовых линий ; если в пределах данного участка грузовая эпюра линейна, то безразлично, умножается ли площадь грузовой эпюры на ординату единичной или, наоборот, площадь единичной эпюры на ординату грузовой; поетроенные эпюры и не штрихуют.