- •1. Задачи теории пластичности. Диаграммы деформирования материалов. Обратимая и необратимая части деформаций, остаточные напряжения и деформации.
- •3. Условные и истинные напряжения и деформации. Условный предел текучести. Эффект Баушингера.
- •4. Условия начала пластического течения. Поверхности пластичности в пространстве напряжений. Условие Треска – Сен-Венана.
- •5. Условия начала пластического течения. Поверхности пластичности в пространстве напряжений. Условие Хубера – Мизеса – Генке. Варианты условий пластичности для анизотропных тел.
- •6. Диаграммы деформирования материалов, методы их построения и схематизация. Основные модели пластических сред.
- •7. Девиаторы напряжений и деформаций. Интенсивности напряжений и деформаций. Гипотеза единой кривой.
- •8. Теория малых упругопластических деформаций а.А. Ильюшина. Гипотезы. Определяющие соотношения. Функция пластичности Ильюшина.
- •9. Понятие простого и сложного нагружения. Теорема о простом нагружении.
- •10. Теоремы теории малых упругопластических деформаций а.А. Ильюшина.
- •11. Итерационные методы решения задач теории пластичности. Метод переменных параметров упругости. Метод дополнительных напряжений. Метод дополнительных деформаций.
- •12. Деформационная теория пластичности анизотропных сред б.Е. Победри. Варианты определяющих соотношений для трансверсально-изотропных и ортотропных материалов. Функции пластичности и их аргументы.
- •13. Свойство ползучести материалов. Расчет деформаций при ползучести.
- •14. Свойство релаксации. Расчет напряжений при релаксации.
- •15. Структурные модели вязкоупругого поведения материалов. Уравнение Кельвина.
- •16. Влияние режимов нагружения на релаксационные процессы. Описание процессов ползучести при нагружении с различной скоростью.
- •17. Влияние режимов нагружения на релаксационные процессы. Описание процессов релаксации при деформировании с различной скоростью
- •18. Деформирование вязкоупругих материалов при различных температурах. Температурно-временная аналогия.
- •19. Уравнения теории вязкоупругости анизотропных сред в условиях сложного напряженного состояния.
13. Свойство ползучести материалов. Расчет деформаций при ползучести.
Одним из ярких проявлений свойств вязкоупругости является ползучесть.
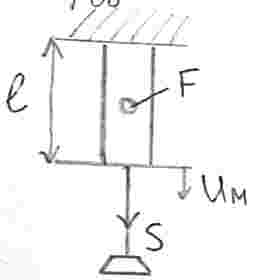
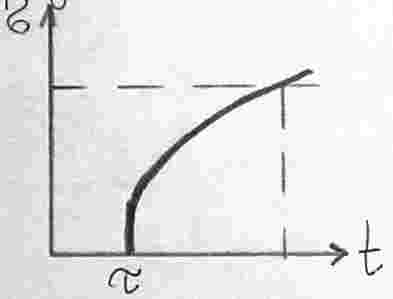
Ползучесть – изменение деформации с течением времени при неизменной нагрузке.
|
|
Опыт на ползучесть.
|
Если
|
![]() ,
где
,
где
![]() - длительный модуль.
- длительный модуль.
|
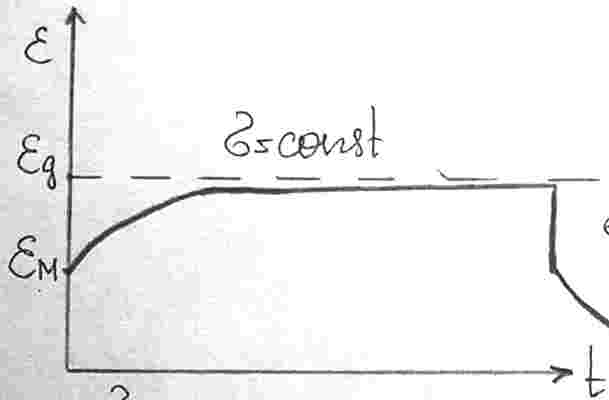
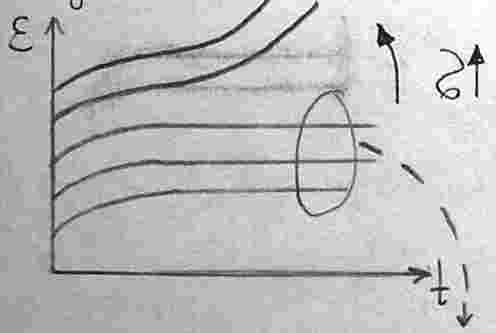
Если
напряжение не очень большое, то кривые
подобны
|
Если нагрузка приложена не в начальный момент времени, то необходимо различать два времени:
![]() - время наблюдения;
- время наблюдения;
![]() - время приложения
нагрузки.
- время приложения
нагрузки.
![]() .
.
Вместо двойного аргумента можно использовать разностный аргумент, но только в том случае, если свойства материала не зависят от времени.
Рассмотрим случай,
когда
![]() зависит от времени (зависимость задаем
самостоятельно).
зависит от времени (зависимость задаем
самостоятельно).
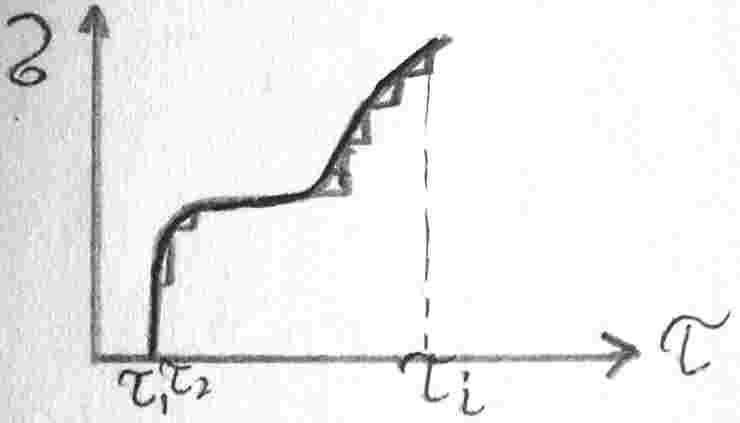
Разобьем нагружение на части. Предположим независимость действия этих нагружений, тогда
![]()
![]()
![]()
![]()
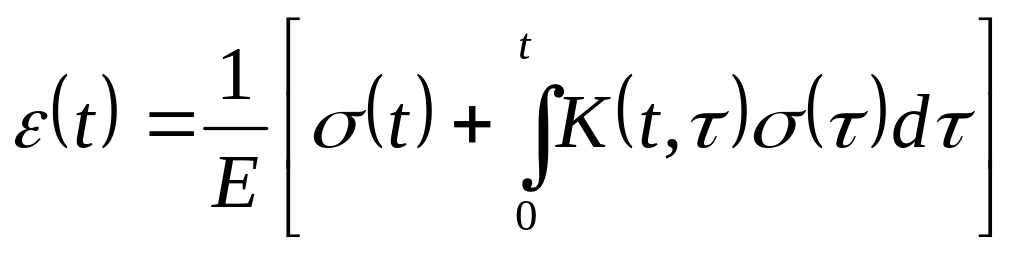 -
-
- интегральное уравнение ползучести (уравнение Вольтерра).
Это интегральное уравнение позволяет определить деформацию в любой момент времени, если задана программа нагружения.
![]() - ядро ползучести
(функция, отражающая свойства материала
и строящаяся на основе эксперимента).
- ядро ползучести
(функция, отражающая свойства материала
и строящаяся на основе эксперимента).
В том случае если
свойства материала не зависят от времени,
то
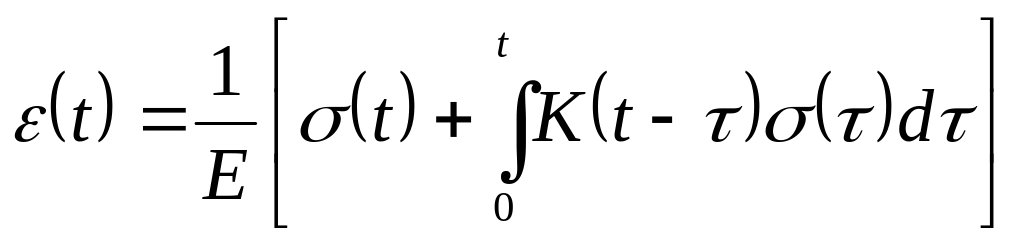
14. Свойство релаксации. Расчет напряжений при релаксации.
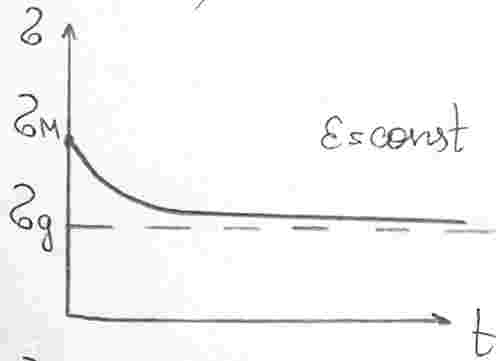
В материале, обладающем свойством ползучести, постоянной деформации соответствует изменение напряжений.
|
|
Если нагрузка приложена не в начальный момент времени, то необходимо различать два времени:
|
- время наблюдения; - время приложения нагрузки.
|
Вместо двойного аргумента можно использовать разностный аргумент, но только в том случае, если свойства материала не зависят от времени.
Рассмотрим случай, когда
![]() зависит от времени (зависимость задаем
самостоятельно).
зависит от времени (зависимость задаем
самостоятельно).
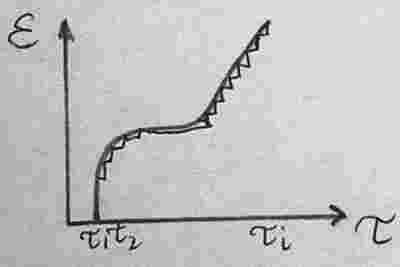
Разобьем деформации на части. Предположим независимость действия этих деформаций, тогда
![]()
![]()
![]()
![]()
 -
-
- интегральное уравнение релаксации (уравнение Вольтерра).
Это интегральное уравнение позволяет определить напряжения в любой момент времени, если задан закон деформирования.
![]() - ядро релаксации (функция, отражающая
свойства материала и строящаяся на
основе эксперимента).
- ядро релаксации (функция, отражающая
свойства материала и строящаяся на
основе эксперимента).
В том случае если свойства материала не зависят от времени, то
 .
.
Материалы, которым свойственны явления ползучести и релаксации, называются реономными. Материалы, у которых напряжения определяются значениями деформаций только в настоящий момент времени, называются склерономными.
15. Структурные модели вязкоупругого поведения материалов. Уравнение Кельвина.
Модели:
|
|
|
|
|
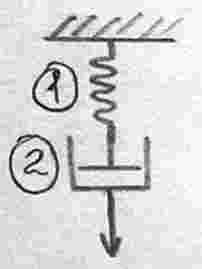
Модель Максвелла.
|
|
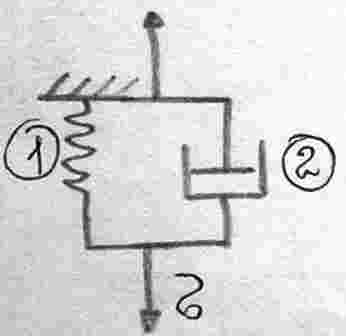
Модель Фойгта.
|
|
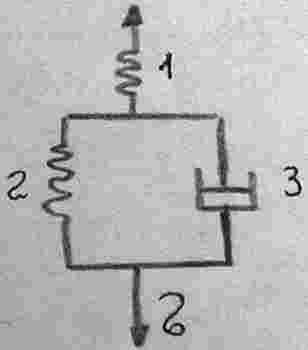
Модель Кельвина.
|
|
![]() - уравнение Кельвина.
- уравнение Кельвина.
Если процесс нагружения (деформирования) происходит очень быстро, то
![]() ,
тогда
,
тогда
![]()
Если процесс нагружения (деформирования) происходит очень медленно, то
![]()
![]() ,
где
-
длительный модуль.
,
где
-
длительный модуль.
Пусть
![]() ,
тогда уравнение Кельвина будет иметь
вид:
,
тогда уравнение Кельвина будет иметь
вид:
![]() ,
,
общим решением этого уравнения является:
 ,
,
в момент времени
![]()
![]()
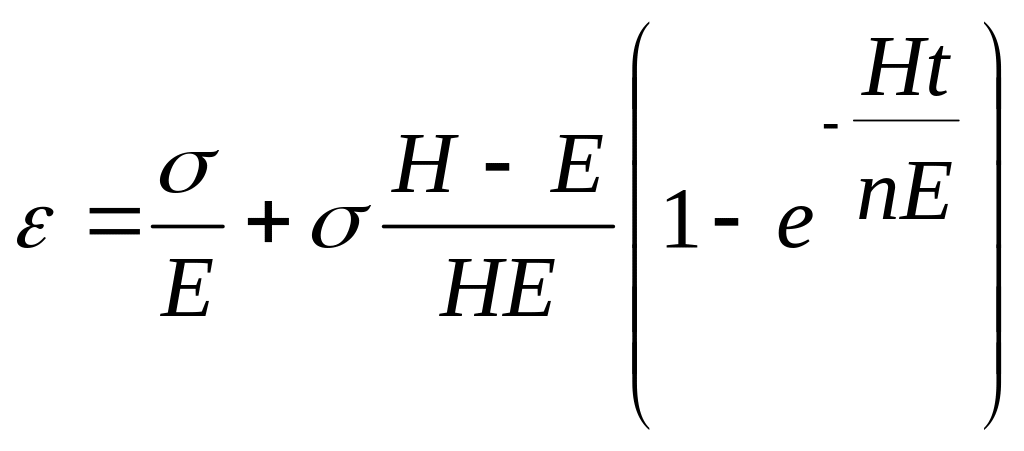 ,
,
при . Это уравнение описывает явление ползучести.
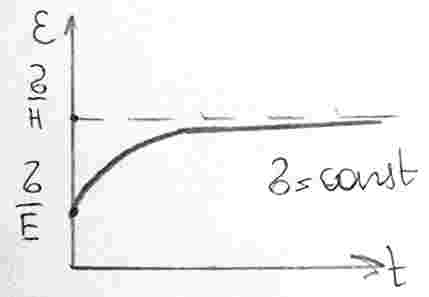
Пусть
![]() ,
тогда
,
тогда
![]() ,
,
общее решение выглядит:
![]() ,
,
в момент времени![]()
![]()
![]() ,
,
это уравнение описывает явление релаксации.

Решение уравнения Кельвина в общем виде:
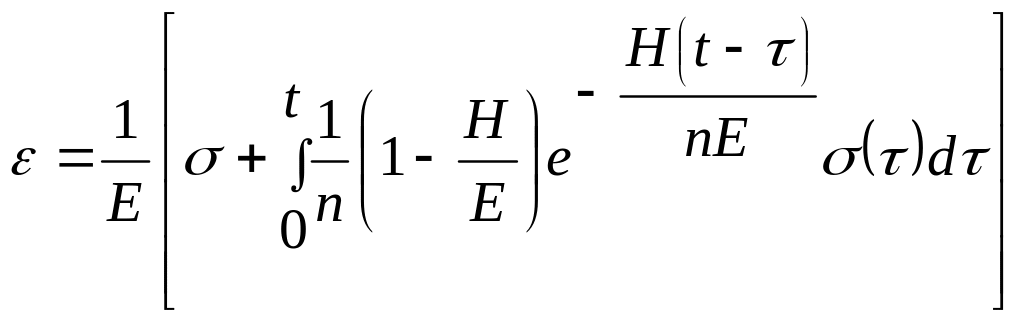 ,
,
где
 - ядро ползучести.
- ядро ползучести.
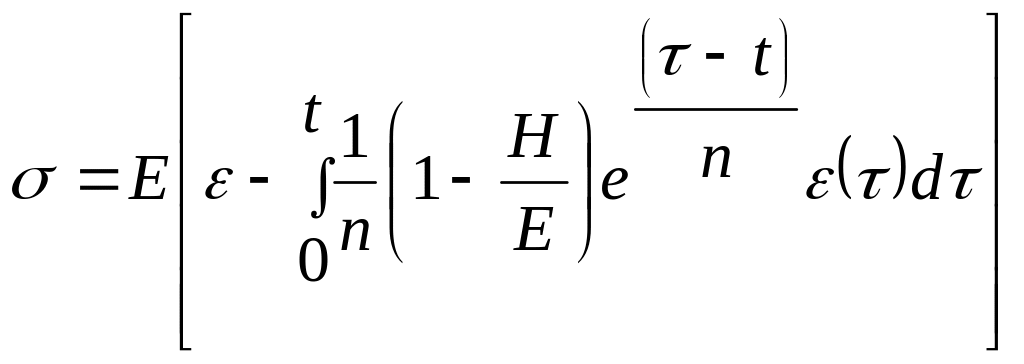 ,
,
где
![]() - ядро релаксации.
- ядро релаксации.
Если переписать уравнения с учетом ядер, то получим уравнения Вольтерра второго рода. Т.о. уравнение Кельвина эквивалентно уравнениям Вольтерра с ядрами релаксации и ползучести экспоненциального типа.