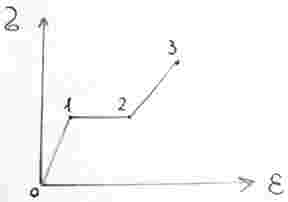
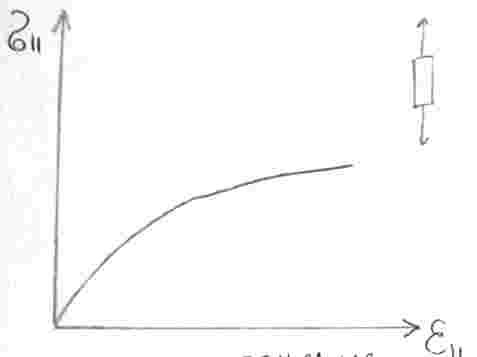
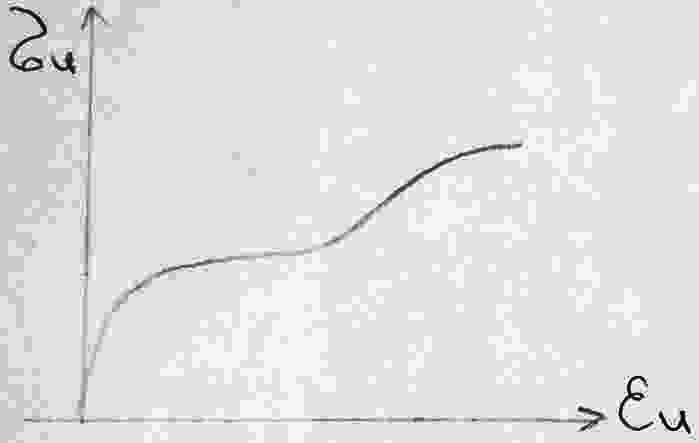
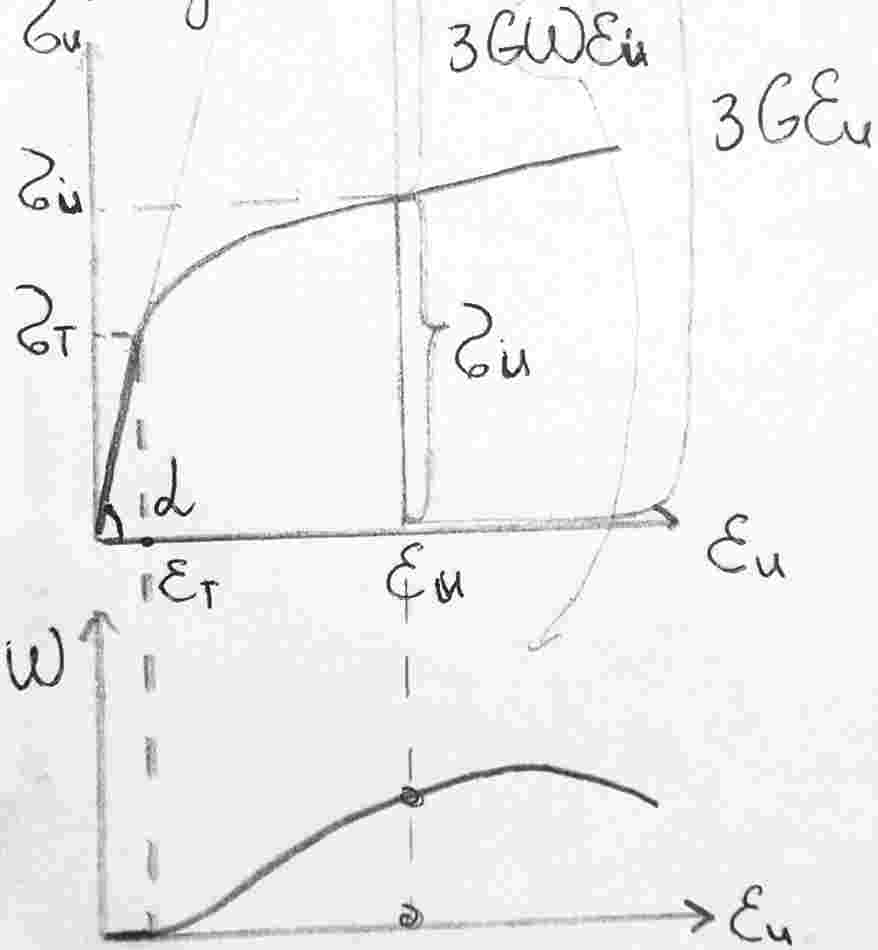
6. Диаграммы деформирования материалов, методы их построения и схематизация. Основные модели пластических сред.

	- напряжения; - деформация - предел прочности - предел пропорциональности - предел упругости - предел текучести
	0–1 – участок упругого деформирования 1–2 – участок идеального пластического деформирования 2–3 – участок упрочнения

Основные модели пластических сред.

1. модель идеального жесткопластического материала.

2. модель идеальной упругопластической среды.

3. модель идеальной упругопластической среды с линейным упрочнением.

   - модуль упрочнения

4. модель упругопластической среды с нелинейным упрочнением.

могут быть и другие

7. Девиаторы напряжений и деформаций. Интенсивности напряжений и деформаций. Гипотеза единой кривой.

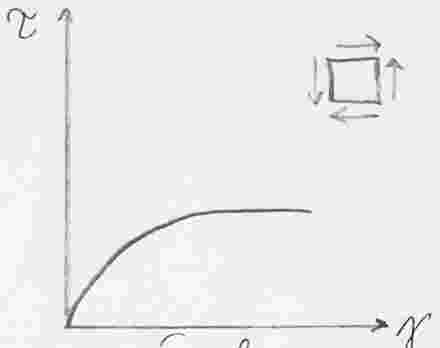
Одноосное растяжение	Чистый сдвиг	Двуосное растяжение или сжатие

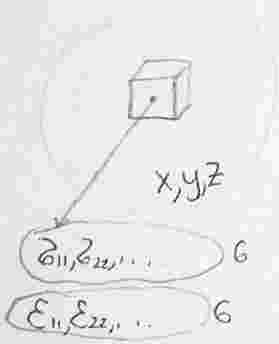
Рассмотрим вторые инварианты (интенсивности) тензоров напряжений и деформаций.

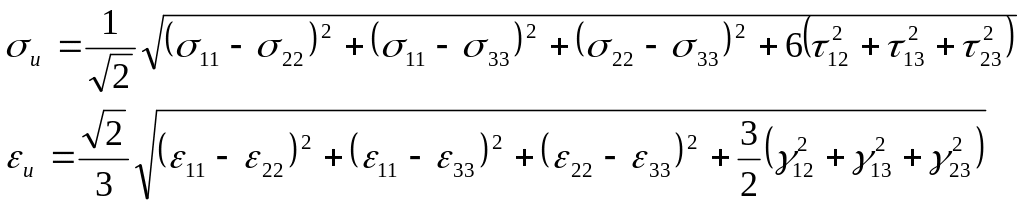
- девиатор тензора напряжений.

- девиатор тензора деформаций.

Теория упругости:

В случае чистого сдвига:

, где

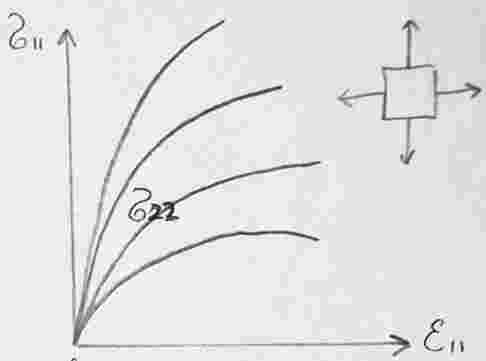
Гипотеза единой кривой.

Предполагается, что существует универсальная функциональная зависимость интенсивности напряжений от интенсивности деформаций (графическое выражение – диаграмма деформирования) независящая от вида НДС.

Эксперимент на одноосное растяжение: , остальные Коэффициент Пуассона может меняться, но в пластичности предполагают, что .

8. Теория малых упругопластических деформаций а.А. Ильюшина. Гипотезы. Определяющие соотношения. Функция пластичности Ильюшина.

Гипотезы:

1. в результате пластической деформации изменения объема не происходит

,

а также предполагается что материал несжимаемый

2. между интенсивностями напряжений и деформаций существует функциональная связь, которая записывается определенным образом

3. компоненты тензора напряжений пропорциональны компонентам тензора деформаций (определяющие соотношения – тензорно-линейные)

;

при чистом сдвиге

;

Гипотезы теории малых упругопластических деформаций были подтверждены экспериментально для металлов при простых нагружениях.

Функция пластичности Ильюшина.

- функция пластичности Ильюшина Если задать функцию, модуль сдвига, предел текучести, мы однозначно определим диаграмму деформирования.

9. Понятие простого и сложного нагружения. Теорема о простом нагружении.

Простой процесс нагружения – это процесс при котором все компоненты тензора напряжений изменяются пропорционально одному параметру.

- параметр процесса, - заданные тензоры.

Простому процессу нагружения в пространстве напряжений соответствует траектория в виде прямой линии.

При сложном нагружении направления главных осей и взаимоотношения главных напряжений могут изменяться.

Теорема о простом нагружении.

Для того чтобы во всех точках несжимаемого тела нагруженного внешними силами, изменяющимися пропорционально одному параметру, нагружение было простым, достаточно, чтобы интенсивности напряжений от интенсивности деформаций была степенной функцией.

- непрерывно возрастающий параметр процесса