
- •Оглавление
- •1.1. Обыкновенные дифференциальные уравнения. Основные понятия
- •1.2. Обыкновенные дифференциальные уравнения 1-го порядка
- •1.3. Дифференциальные уравнения 1-го порядка с разделяющимися переменными
- •1.4. Однородные дифференциальные уравнения 1-го порядка
- •1.5. Дифференциальные уравнения, приводящиеся к однородным
- •1.6. Обобщенное однородное уравнение
- •1.7. Линейные дифференциальные уравнения 1-го порядка
- •1.8. Уравнение Бернулли
- •1.9. Дифференциальные уравнения в полных дифференциалах
- •1.10. Интегрирующий множитель
- •2. Дифференциальные уравнения 2-го порядка
- •2.1. Методы понижения порядка уравнения
- •2.2. Линейное дифференциальное уравнение 2-го порядка
- •2.3. Определитель Вронского
- •2.4. Структура общего решения лоду 2-го порядка
- •2.5. Лоду 2-го порядка с постоянными коэффициентами
- •2.6. Структура общего решения лнду 2-го порядка
- •2.7. Решение лнду 2-го порядка с постоянными коэффициентами со специальной правой частью
- •2.8. Метод вариации произвольных постоянных (метод Лагранжа)
- •3. Линейные уравнения высших порядков
- •3.1. Однородное уравнение
- •3.2. Линейное однородное дифференциальное уравнение с постоянными коэффициентами
- •4. Системы обыкновенных дифференциальных уравнений
- •4.1. Нормальные системы
- •4.2. Метод исключения
- •4.3. Линейные однородные системы дифференциальных уравнений (лос ду)
- •4.4. Лос ду с постоянными коэффициентами
- •4.5. Линейные неоднородные системы дифференциальных уравнений (лнс ду)
- •4.6. Метод вариации произвольных постоянных
2.6. Структура общего решения лнду 2-го порядка
Теорема 1. Общее решение ЛНДУ 2-го порядка
 (6.1)
(6.1)
представляется
в виде суммы общего решения
 соответствующего однородного уравнения
соответствующего однородного уравнения
 (6.2)
(6.2)
и
любого частного решения

 уравнения (6.1).
уравнения (6.1).
Доказательство.
Докажем
сначала, что

 будет решением уравнения (6.1). Для этого
подставим
в уравнение (6.1):
будет решением уравнения (6.1). Для этого
подставим
в уравнение (6.1):

 .
.
Это равенство
является тождеством, так как

 и
и

 .
Следовательно,
есть решение уравнения (6.1).
.
Следовательно,
есть решение уравнения (6.1).
Докажем теперь, что это решение является общим, т.е. можно так выбрать входящие в него произвольные постоянные, что будут удовлетворяться любые начальные условия вида:
 ,
,
 .
.  (6.3)
(6.3)
Согласно теореме о структуре общего решения линейного однородного дифференциального уравнения общее решение уравнения (6.2) можно представить в виде:

 ,
,
где
 и
и
 – линейно независимые решения этого
уравнения.
– линейно независимые решения этого
уравнения.
Таким образом:

 и, следовательно, начальные условия
(6.3) можно записать в виде:
и, следовательно, начальные условия
(6.3) можно записать в виде:

или
 (6.4)
(6.4)
Произвольные
постоянные
и
определяются из этой системы линейных
алгебраических уравнений однозначно
при любых правых частях, так как
определитель этой системы
 есть значение определителя Вронского
для линейно независимых решений уравнения
(6.2) при
,
а такой определитель, как было указано
выше, отличен от нуля. Определив постоянные
и
из системы уравнений (6.4) и подставив их
в выражение
,
мы получим частное решение уравнения
(6.1), удовлетворяющее заданным начальным
условиям. Теорема доказана.
есть значение определителя Вронского
для линейно независимых решений уравнения
(6.2) при
,
а такой определитель, как было указано
выше, отличен от нуля. Определив постоянные
и
из системы уравнений (6.4) и подставив их
в выражение
,
мы получим частное решение уравнения
(6.1), удовлетворяющее заданным начальным
условиям. Теорема доказана.
Теорема
2. Если
 – решение дифференциального уравнения
– решение дифференциального уравнения
 ,
,
а

 – решение уравнения
– решение уравнения
 ,
,
то
функция

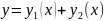 является решением уравнения
является решением уравнения
 . (6.5)
. (6.5)
Доказательство.
Подставив
функцию  в уравнение (6.5), получим
в уравнение (6.5), получим
 .
.
Это равенство является тождеством, так как
 и
и
 .
.
Теорема доказана.
2.7. Решение лнду 2-го порядка с постоянными коэффициентами со специальной правой частью
Рассмотрим случай, когда коэффициенты в уравнении (6.1) постоянны, т.е. уравнение имеет вид:
 ,
, (7.1)
(7.1)
где

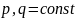 .
.
Рассмотрим метод
отыскания частного решения

 уравнения (7.1) в случае, когда правая
часть
имеет специальный
вид. Это метод называется методом
неопределённых коэффициентов
и состоит в подборе частного решения в
зависимости от вида правой части
.
Рассмотрим правые части уравнения (7.1)
следующего вида:
уравнения (7.1) в случае, когда правая
часть
имеет специальный
вид. Это метод называется методом
неопределённых коэффициентов
и состоит в подборе частного решения в
зависимости от вида правой части
.
Рассмотрим правые части уравнения (7.1)
следующего вида:
 ,
где
,
где
 – многочлен степени
– многочлен степени
 ,
причём некоторые коэффициенты, кроме
,
причём некоторые коэффициенты, кроме
 ,
могут равняться нулю. Укажем вид частного
решения в этом случае.
,
могут равняться нулю. Укажем вид частного
решения в этом случае.
Если число
 не является корнем характеристического
уравнения (5.2), то частное решение
записываем в виде:
не является корнем характеристического
уравнения (5.2), то частное решение
записываем в виде:

 ,
,
где

 – неопределённые коэффициенты, которые
подлежат определению методом неопределённых
коэффициентов.
– неопределённые коэффициенты, которые
подлежат определению методом неопределённых
коэффициентов.
Пример
1.
Найти общее решение уравнения

 .
.
Решение. Для
уравнения

 составляем характеристическое уравнение:
составляем характеристическое уравнение:

 .
Откуда получаем
.
Откуда получаем
 .
Следовательно, общее решение однородного
уравнения есть
.
Следовательно, общее решение однородного
уравнения есть

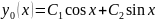 .
.
Правая часть
заданного уравнения
 имеет специальный вид (случай 1), причём
имеет специальный вид (случай 1), причём

 не является корнем характеристического
уравнения, поэтому частное решение ищем
в виде:
не является корнем характеристического
уравнения, поэтому частное решение ищем
в виде:

 ,
,
где A, B – неопределённые коэффициенты.
Найдём производные первого и второго порядков и подставим их в заданное уравнение:

 .
.
Сократим обе части
на

 и приравняем коэффициенты при одинаковых
степенях x
в левой и правой частях равенства:
и приравняем коэффициенты при одинаковых
степенях x
в левой и правой частях равенства:


Из полученной
системы уравнений находим:

 .
Тогда
.
Тогда
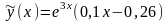
 ,
а общее решение заданного уравнения
есть:
,
а общее решение заданного уравнения
есть:

 .
.
Если является корнем кратности

 соответствующего характеристического
уравнения, то частное решение ищем в
виде:
соответствующего характеристического
уравнения, то частное решение ищем в
виде:

 ,
,
где – неопределённые коэффициенты, которые подлежат дальнейшему определению.
Пример
2.
Решить уравнение
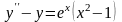
 .
.
Решение.
Соответствующее
характеристическое уравнение имеет
вид:

 ,
откуда
,
откуда

 .
Тогда общее решение однородного уравнения
.
Тогда общее решение однородного уравнения
 есть:
есть:

 .
.
Правая
часть заданного уравнения имеет
специальный вид (случай 1).
Так как

 является корнем характеристического
уравнения кратности
является корнем характеристического
уравнения кратности

 ,
то частное решение ищется в виде:
,
то частное решение ищется в виде:
 .
.
Находим неопределённые
коэффициенты A,
B,
C
методом, изложенным в примере 1. В
результате получаем

 .
Окончательно имеем следующее выражение
для общего решения:
.
Окончательно имеем следующее выражение
для общего решения:

 .
.
Правая часть
 ,
где хотя бы одно из чисел M
и N
отлично от нуля. Укажем вид частного
решения в этом случае.
,
где хотя бы одно из чисел M
и N
отлично от нуля. Укажем вид частного
решения в этом случае.
Если число

 не является корнем характеристического
уравнения (5.2), то частное решение ищем
в виде:
не является корнем характеристического
уравнения (5.2), то частное решение ищем
в виде:

 ,
,
где A, B – неопределённые коэффициенты.
Если число является корнем характеристического уравнения (5.2), причём кратность этого корня , то запишем частное решение в виде:

 ,
,
где A, B – неопределённые коэффициенты.
Пример
3.
Решить уравнение

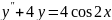 .
.
Решение.
Корнями
характеристического уравнения для

 являются комплексно-сопряженные числа
являются комплексно-сопряженные числа

 .
В этом случае общее решение этого
уравнения:
.
В этом случае общее решение этого
уравнения:

 .
.
Правая часть заданного в примере 3 уравнения имеет специальный вид:
 ,
,
где

 ,
а
,
а
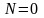
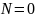 .
Число
.
Число

 является корнем характеристического
уравнения кратности
,
поэтому частное решение исходного
уравнения примет вид:
является корнем характеристического
уравнения кратности
,
поэтому частное решение исходного
уравнения примет вид:

 .
.
Для
определения A
и B
находим
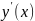 ,
,

 и подставляем в заданное уравнение:
и подставляем в заданное уравнение:

 .
.
Приводя
подобные члены, приравнивая коэффициенты
при
 и
и
 ,
получаем следующую систему:
,
получаем следующую систему:

 ,
,
откуда

 .
.
Окончательно общее решение заданного уравнения имеет вид:

 .
.
 ,
где
,
где

 и
и

 –
многочлены степени p
и q
соответственно, причём один из этих
многочленов может равняться нулю.
Укажем вид частного решения в этом
общем случае.
–
многочлены степени p
и q
соответственно, причём один из этих
многочленов может равняться нулю.
Укажем вид частного решения в этом
общем случае.
Если число

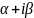 не является корнем характеристического
уравнения (5.2), то вид частного решения
будет следующим:
не является корнем характеристического
уравнения (5.2), то вид частного решения
будет следующим:
 ,
,  (7.2)
(7.2)
где
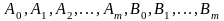
 – неопределённые коэффициенты, а
– неопределённые коэффициенты, а

 .
.
Если число является корнем характеристического уравнения (5.2) кратности , то частное решение ЛНДУ примет вид:
 , (7.3)
, (7.3)
т.е.
частное решение вида (7.2) надо умножить
на

 .
В выражении (7.3)
.
В выражении (7.3)

 – многочлены с неопределёнными
коэффициентами, причём их степень
.
– многочлены с неопределёнными
коэффициентами, причём их степень
.
Пример 4. Указать вид частного решения для уравнения

 .
.
Решение.
Характеристическое
уравнение имеет вид:

 .
Его корни:
.
Его корни:
 .
Общее решение ЛОДУ имеет вид:
.
Общее решение ЛОДУ имеет вид:

 .
.
Правая
часть заданного уравнения имеет
специальный вид (случай 3):
 .
Число
.
Число

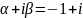 является корнем характеристического
уравнения кратности
.
Коэффициент при
является корнем характеристического
уравнения кратности
.
Коэффициент при

 является многочленом первой степени,
а при
является многочленом первой степени,
а при

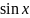 – нулевой степени, поэтому степень
многочленов с неопределёнными
коэффициентами надо брать
– нулевой степени, поэтому степень
многочленов с неопределёнными
коэффициентами надо брать

 .
.
Итак, вид частного решения:

 .
.
Коэффициенты A, B, C, D могут быть определены по методу неопределённых коэффициентов.
Замечание.
Если правая часть уравнения (7.1) есть
сумма двух функций
 ,
причём каждая из функций
,
причём каждая из функций
 ,
,
 имеет специальный вид (случаи 1-3), то
частное решение
подбирается в виде суммы:
имеет специальный вид (случаи 1-3), то
частное решение
подбирается в виде суммы:
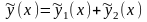
 ,
где
,
где
 есть частное решение для уравнения с
правой частью
,
а
есть частное решение для уравнения с
правой частью
,
а

 есть частное решение для уравнения с
правой частью
.
есть частное решение для уравнения с
правой частью
.
Аналогично находятся частные решения в случае, когда правая часть уравнения есть алгебраическая сумма конечного числа функций специального вида, рассмотренного в случаях 1-3.
