4.2. Метод исключения
Продифференцируем, например, первое уравнение системы уравнений (4.2) по независимой переменной x:
.
Вместо системы (4.2) запишем систему уравнений:
(4.3)
Из первого уравнения
системы (4.3) следует, что
.
Подставим эту функцию во второе уравнение
системы (4.3):
.
Итак, исключив из
системы функцию z
приходим к одному уравнению 2-го порядка,
решая которое, получаем:
.
Теперь продифференцируем
найденное выражение по x
и подставим в функцию
,
получим
.
В результате заключаем, что решение примет вид:
(4.4)
Определение. Общим решением системы двух обыкновенных дифференциальных уравнений 1-го порядка является совокупность функций (4.4), непрерывно дифференцируемых на некотором интервале , которые при различных допустимых значениях произвольных постоянных удовлетворяют обоим уравнениям системы уравнений (4.2). При этом в области, в которой выполнены условия теоремы существования и единственности, можно получить решение любой задачи Коши.
4.3. Линейные однородные системы дифференциальных уравнений (лос ду)
Определение. Линейной однородной системой дифференциальных уравнений (ЛОС ДУ) для функций называется система уравнений вида
(4.5)
где
– непрерывные на некотором интервале
функции.
Свойства решений ЛОС ДУ (4.5).
Сумма двух решений системы (4.5) – тоже решение этой системы.
Доказательство:
Пусть
и
– два каких-либо решения системы (4.5).
Тогда
Но
и
.
Аналогично рассматривается и второе уравнение системы (4.5).
Если – решение ЛОС ДУ и c – произвольная константа, то
– тоже решение (4.5).
Доказательство свойства аналогично доказательству свойства 1.
Следствие.
Если
и
– решения системы (4.5), то выражение вида
где
– произвольные постоянные, тоже решение
(4.5).
Определение 1. Система функций и называется линейно независимой на некотором интервале , если из системы равенств
(4.6)
следует,
что
.
В противном случае система функций и называется линейно зависимой на интервале .
Определение 2. Определитель, составленный для системы функций и , называется определителем Вронского и обозначается W(x), т.е.
.
Теорема 1. Определитель Вронского для линейно независимой на интервале системы решений и ЛОС ДУ не равен нулю ни в одной точке интервала .
Доказательство.
Докажем теорему методом от противного.
Предположим, что существует точка
,
в которой
.
Составим линейную
однородную систему уравнений с
неизвестными
и 
:
. (4.7)
Так как определитель
системы (4.7) равен нулю, то система имеет
бесконечное множество ненулевых решений.
Пусть
– одно из них. С помощью этих констант
и двух линейно независимых на интервале
решений системы (3.1)
и
составим две функции
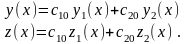(4.8)
Согласно следствию из свойств решений ЛОС ДУ функции (4.8) являются решениями системы (4.5), которые в силу равенств (4.7) в точке обращаются в нуль. Следовательно, – решение следующей задачи Коши:
Но таким решением
может быть только нулевое решение:
при любом
,
т.е.
Причём
.
Это означает, что система функций
и
линейно зависима на интервале
,
что противоречит условию теоремы. Значит
наше предположение о существовании на
интервале
точки
,
в которой
,
неверно, что и доказывает теорему.
Определение 2. Линейно независимые на интервале решения ЛОС ДУ и называются фундаментальной системой решений системы уравнений (4.5).
Теорема 2. Если семейство функций и образует фундаментальную систему решений ЛОС ДУ (4.5), то их линейная комбинация
, (4.9)
где – произвольные постоянные, даёт общее решение системы (4.5).
Доказательство.
Равенства (4.9), согласно следствию из свойств решений ЛОС ДУ, определяют решение системы уравнений (4.5).
Докажем, что равенства (4.9) определяют общее решение (4.5), для этого докажем, что каковы бы ни были начальные условия задачи Коши , всегда найдутся значения постоянных такие, что выделенное из общего частное решение ЛОС ДУ
будет удовлетворять этим условиям.
Для этого подставим в равенства (4.9) начальные условия, получим:
(4.10)
Определителем этой алгебраической системы линейных уравнений является определитель Вронского :
,
который, согласно теореме 1, не равен нулю. Следовательно, система уравнений (4.10) имеет решение и притом единственное.