
- •Основные задачи динамики вагонов.
- •Основные этапы решения задач по динамике вагонов.
- •Основные причины колебания вагонов.
- •Угловые перемещения колесной пары
- •Виды колебаний
- •Динамические характеристики верхнего строения пути.
- •Стрелочные переводы.
- •Виды колебаний.
- •Характеристики элементов соединений.
- •Принцип Даламбера.
- •Вынужденные колебания простейшей системы.
- •Динамическая модель вагона.
- •Составление уравнений вертикальных колебаний моделей с одной степенью свободы при кинематическом возмущении.
- •Расчет параметров гасителей колебаний простейшей колебательной системы.
- •Свободные колебания в недемпфированной системе.
- •Свободные колебания в системе с гидравлическим гасителем колебаний.
- •Матричная форма записи уравнений колебаний.
- •Принцип составления уравнений колебаний в матричной форме на примере одноосной модели с двумя степенями свободы.
- •Правило записи в матричную форму.
- •Вынужденные колебания динамических систем.
- •Частотный метод исследования вынужденных колебаний.
- •Кинематическое описание процесса качения колесных пар по рельсам. Расчетная схема.
- •Меры принимаемые для снижения интенсивности извилистого движения подвижного состава.
- •Упругое проскальзывание. Смещение волокон колеса и рельса при образовании контактного пятна.
Принцип Даламбера.
Материальная точка под действием силы Fa движется по связи. Ускорение направлено по равнодействующей силе R , векторная сумма активной силы Fa и силы реакции N определяется

тогда


Если к действующей на тело активной силе и реакции связи приложить дополнительную силу инерции, то тело будет находиться в равновесии (сумма всех сил действующих в системе дополнительная главным вектором инерции равна нулю).
Данный принцип придает уравнениям движения формальный вид уравнений равновесия.

Согласно принципу Даламбера после добавления сил инерции система находится в равновесии.



Груз нужно поднимать с минимальной скоростью.
Вынужденные колебания простейшей системы.
Изобразим движение подвешенной на колесе массы m, когда колесо катится по жесткому пути, имеющему неровности косинусоидальной формы.

В
этой системе силы инерции массы m,
т.е.
 ,
уравновешиваются силами, возникающими
при деформации рессоры (z
– zk),
т.е. силой ж(z
– zk).
,
уравновешиваются силами, возникающими
при деформации рессоры (z
– zk),
т.е. силой ж(z
– zk).
Используя принцип Даламбера

С
учетом
 проведем преобразование данного
уравнения:
проведем преобразование данного
уравнения:

Поделив все члены этого уравнения на m, получим

где
 – круговая частота свободных колебаний
системы.
– круговая частота свободных колебаний
системы.
Общее решение этого уравнения с правой частью (неоднородного) можно представить как сумму решения однородного уравнения z1 и частного решения неоднородного уравнения z2, т.е. z=z1+z2.
Найдем вначале частное решение уравнения. Допустим

и подставим его в общее уравнение:

Откуда
 т.е.
т.е.
 .
.
Решение однородного уравнения можно представить в виде:

Тогда общее решение уравнения представляется как
 .
.
Начало отсчета времени (t=0) в этой системе можно принять для такого момента, когда z=0. Подставив, получим
 ,
,
Откуда
 .
.
Подставляя А1 в основное уравнение, получим

Величину
 называют
коэффициентом
нарастания колебаний.
называют
коэффициентом
нарастания колебаний.
Приняв это значение, уравнение запишется
 .
.
Это и будет общим решением нашего уравнения при принятых выше начальных условиях.
Исследуем
поведение колебательной системы в том
случае, когда частота возмущений
 приближается к частоте собственных
колебаний
приближается к частоте собственных
колебаний
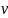 .
.
Для удобства дальнейшего анализа формулу (1.47) представим в следующем виде:

Обозначая
 =
2ε, подставим
это выражение в предыдущую формулу
и, полагая, что
=
2ε, подставим
это выражение в предыдущую формулу
и, полагая, что
 ,
получим
,
получим

Преобразуем

Поскольку ε малая величина, то ее период T1 весьма велик и значительно больше периода T2, определяемого частотой возмущений за счет неровностей ω.
Это
позволяет рассматривать такие колебания
(при близких ω и
),
как
колебания с частотой ω и с переменной
амплитудой. Такие колебания называют
биением
с
периодом
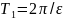 .
С
приближением ω
к
ν
.
С
приближением ω
к
ν
 п
п ериод
Т1
увеличивается. При точном совпадении
величин v
и
ω
наступает явление резонанса.
ериод
Т1
увеличивается. При точном совпадении
величин v
и
ω
наступает явление резонанса.
Биение Резонанс
Динамическая модель вагона.
Для исследования динамических свойств вагонов составляют его механическую модель.
Механико-математической (динамической) моделью называют механическую модель вагона описанную системой дифференциальных уравнений.
Динамическая модель должна отражать основные свойства рассматриваемой системы в такой степени, чтобы с её помощью можно было с требуемой точностью оценить динамические качества вагона.
Модель вагона характеризуется набором следующих параметров:
инерционные характеристики (массы тел и моменты инерции)
характеристики элементов соединения (жесткости и показатели демпфирования)
геометрические размеры (длина, высота..)
Положение механической системы может определяться набором k независимых параметров различной физической и кинематической природы, к которым относятся:
декартовы координаты точек
расстояния отсчитываемые от траектории
углы поворота
Число k называют числом степеней свободы, а сами параметры обобщенными координатами q. Простейшей динамической моделью является модель с одной степенью свободы.
