59. Функциональные ряды. Основные понятия

Ряд  , члены которого являются функциями от переменной  , называется функциональным.

При различных значениях   из функционального ряда получаются различные числовые ряды, которые могут быть сходящимися или расходящимися.

Если ряд сходится то -наз. точкой сходимости

Если расходится то -наз. Точкой расходимости.

Совокупность числовых значений аргумента , при которых функциональный ряд сходится, наз. Его областью сходимости.

Очевидно, что в области сходимости функционального ряда его сумма является функцией от  . Будем ее обозначать  .

60. Теорема Абеля

Теорема. Если степенной ряд   сходится при x = x₁ , то он сходится и притом абсолютно для всех  .

61. Свойства степенных рядов

1. Сумма S(x) степенного ряда

Является непрерывной функцией в интервале сходимости (-R;R)

2. Степенные ряды ,имеющие радиусы сходимости соотв-о , можно почленно складывать, вычитать и умножать. Радиус сходимости произведения, суммы и разности рядом не меньше чем меньшее из чисел

3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать; при этом для ряда (пиши вместо скобки просто x)

При -R выполняется равенство

4. Степенной ряд можно почленно интегрировать на каждом отрезке, расположенном внутри интервала сходимости; при этом для ряда

(пиши вместо скобки просто x) при -R

62. Ряды Тейлора и Маклорена. Достаточные условия разложимости функции в ряд Тейлора.

Ряд Тейлора:

Ряд Тейлора в окрестности точки a имеет виды:

1) , где f(x) - функция, имеющая при х=а производные всех порядков. R_n - остаточный член в ряде Тейлора определяется выражением 

2)

k-тый коэффициент (при х_k) ряда определяется формулой

Теорема Маклорена (ряд Маклорена (=Макларена)) имеет вид:

1)  , где f(x) - функция, имеющая при а=0 производные всех порядков. R_n - остаточный член в ряде Маклорена (Тейлора при а=0)определяется выражением 

2)

k-тый коэффициент (при х_k) ряда определяется формулой

63) Разложение некоторых элементарных ф-ций в ряде Маклорена

Разложение функции f(x)=e^x в ряд Маклорена:

f(x)=f′(x)=f″(x)=…=f⁽ⁿ⁾(x)=…=e^x.

f(0)=f′(0)=f″(0)=…=f⁽ⁿ⁾(0)=…=1.

Составим для функции f(x)=e^x формально ряд Маклорена:

1+ .

Найдём области сходимости этого ряда.

при любых x, следовательно, областью сходимости ряда является промежуток (-∞;+∞). Заметим, что так как ряд сходится абсолютно, то при любых х и тем более при любых х. Так как f⁽ⁿ⁺¹⁾(x)=e^x и f⁽ⁿ⁺¹⁾(с)=e^с, то =e^c =0. Таким образом, имеет место разложение при x (-∞;+∞)

e^x=1+

64) Применение рядов к приближенным вычислениям значений ф-ции, определённых интегралов

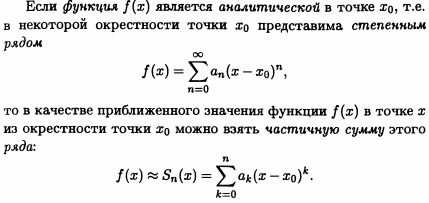
Eсли подинтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью.

Вычислить интеграл с точностью до 0,001. Решение. Проверим, можем ли мы отбросить остаток после второго члена полученного ряда. . Следовательно, .