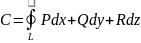35. Основные свойства двойного интеграла.

1.

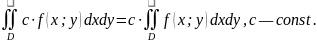
2.

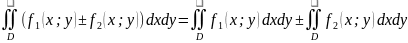
3.

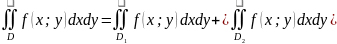
4. Если f(x;y)≥0, . Если f(x;y)≥ φ(x;y),

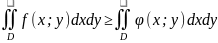
5. 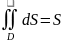т. к.

6. Если f(x;y) непрерывна в замкнутой D, площадь кот. S, то 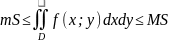, где m и M — соотв. наиб. и наим. значения подынтегральной ф-ции в D.

7. Если f(x;y) непрерывна в замкнутой D, площадь кот. S, то в этой обл-ти Ǝ такая т. (x₀;y₀), что . Величина f(x₀;y₀) = … — среднее значение ф-ции f(x;y) в обл-ти D.

36. Вычисление двойного интеграла в декартовых координатах.

Пусть требуется вычислить 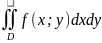, где f(x;y)≥0, непрер. в D. Двойной интеграл выражает объем цилиндрического тела, ограниченного сверху z = f(x;y). Т. к. , S(x) — площадь сечения пл-тью, ﬩ оси Ox, a и b — ур-я пл-тей, огранич. данное тело. D — криволинейная трапеция, правильная относит. Oy, . Согласно методу параллельных сечений 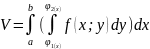. Также объем цил. тела — двойной интеграл от f(x;y)≥0.

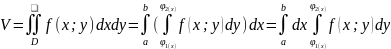
37. Вычисление двойного интеграла в полярных координатах.

x = rcosφ, y = rsinφ, dxdy = rdrdφ.

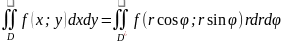
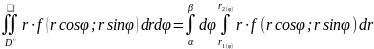
Внутренний интеграл берется при постоянном φ.

38. Приложения двойного интеграла (объем тела, площадь плоской фигуры, масса плоской пластинки, статистические моменты, моменты инерции)

ОБЪЕМ ТЕЛА:

ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ:

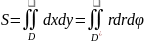
МАССА ПЛОСКОЙ ФИГУРЫ: 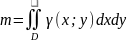. γ = γ(x;y) — плотность

СТАТИСТИЧЕСКИЕ МОМЕНТЫ: 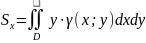и

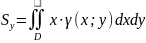
МОМЕНТЫ ИНЕРЦИИ ПЛ. ФИГУРЫ: 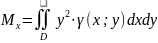и

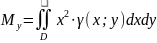
МАССА ПЛОСКОЙ ПЛАСТИНКИ: γ = γ(x;y) — поверхностная плотность — непрер. ф-ция координат т. (x;y). Разобьем пластинку D на n D_i, обозначим их площади через ∆S_i, возьмем M_i(x_i;y_i) и найдем плотность в ней. Плотность в каждой т. D_i const, найдем m_i ≈ γ(x;y)∆S_i. Т. к. m = ∑m_i, m ≈ ∑γ(x;y)∆S_i. n→∞ и maxd_i→0.

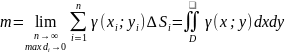
39-40.

х,y,z-const.Отметим,что поскольку разбивать рассм-ую обл.интег.можно произв.образом,то разбивая ее коорд.пов-ми в декарт.сист.коорд.

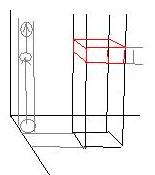Тр.интег.f(x,y,z)dxdydz

DcR

D простая в пространстве будем считать простой в направлении z,если она:

1)проец.на пл-ть Оxy

2)ограничена сверху z=z₂ (x,y),снизу z=z₁(x,y),(x,y)€D

По аналогии с предыд.пол-ем случай правильной обл.D(и по x,y,z прав),получим сведение к 1-му из 6 интег.

тр.интег.f(x,y,z)dxdydz=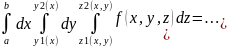

41.Замена переменных в тройном интеграле

Пусть совершена подстановка x= 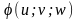, y= , z= . Если эти ф-ции имеют в некоторой области V^* пространства Ouvw непрерывные частные производные и отличный от 0 определитель

,

То справедлива формула:

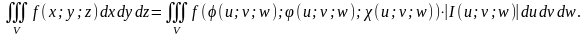
Здесь 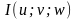 — определитель Якоби, или якобиан преобразования.

42. Приложения тройного интеграла (объем, масса тела, статические моменты, моменты инерции тела).

1. Объем тела

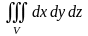— в декартовых координатах

2. Масса тела

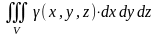, при заданной плотности

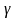
3.Статические моменты (относительно координатных плоскостей)

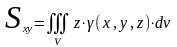
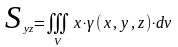
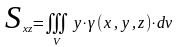
4. Моменты инерции тела

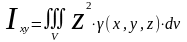
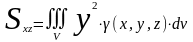
43.кри 1-го рода,их выч-е и св-ва(неориентированная)

В нек.окр.дуги L задано нек.скаляр.поле u=u(M)(1)

u=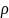 (M)-лин.пл-ть (поле масс)

Задача о массе материал.дуги Lю

Для реш.ввод.скаляр.эл-т дуги.

dS=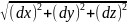 (2)

d=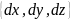

d_m= (M)dS(3)

интегрируем m_L= (4)

Вычисление:Пусть кри L зад-ся парам-ки:

L: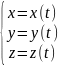 ,t€[t₀,t₁],где ф.x(t),y(t),z(t) предполаг-ся непрерывно диф-ми и в нуль не обращаются

Учитывая,что dS скаляр-й эл-т дуги,в этом случае,= =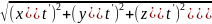 dt,t₀‹t

Сведение кри1 к опред.интег.

, t₀‹t₁

св-ва:во многом аналог.св-вам опред.интег.В частности имеется св-во лин-ти,аддетивности.

После рассматривания этих св-в возник.вопр.,какой из кри более близкий родственник к опред.интег.

Замеч.:если криволин.интег.расс-ся по замкнутой дуге,то

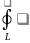
44

45.приложение кри-1 рода

Длина кривой:

Площадь цилиндрической поверхности: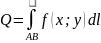

Масса кривой:

Статические моменты:

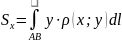
46.условия независимости КРИ-2 от пути интегрирования. Потенциал

Для того чтобы криволинейныйинт. 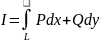не зависел от пути интегрирования в односвязной области D, в которой функции 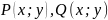непрерывны вместе со своими частными производными, необходимо и достаточно, чтобы в каждой точке этой области выполнялось условие: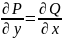

47. Приложения КРИ II рода

Площадь плоской фигуры:

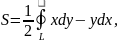
При этом кривая L обходится против часовой стрелки:

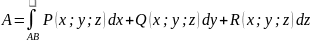
48. Основные понятия теории поля. Потенциальные векторные поля. Циркуляция

Полем называется область V пространства, в каждой точке которой определено значение некоторой величины. Если каждой точке М этой области соотв. Опред. Число U=U(M). Говорят, что в области определено (задано) скалярное поле(или функция точки).Если же каждой точке каждой точке М области пространства соотв. Некоторый вектор 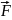то говорят, что задано векторное поле(или векторная функция точки).если скалярное поле не зависит от времени- стационарное. Если меняется с течение времени –нестационарное.

Вектор определяющий векторно поле, можно рассм. как векторную функцию трех скалярных аргументов x,y,z:

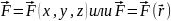
Векторной линией поля 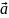наз. Линия, касательная к кот.в точке в каждой точке М имеет направление соотв-его ей вектора

Векторные линии поля:

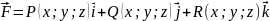
Описываются системой дифференциальных уравнений вида:

=

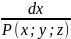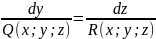
Криволинейный интеграл по замкнутому контуру L наз. Циркуляцией поля вдоль L