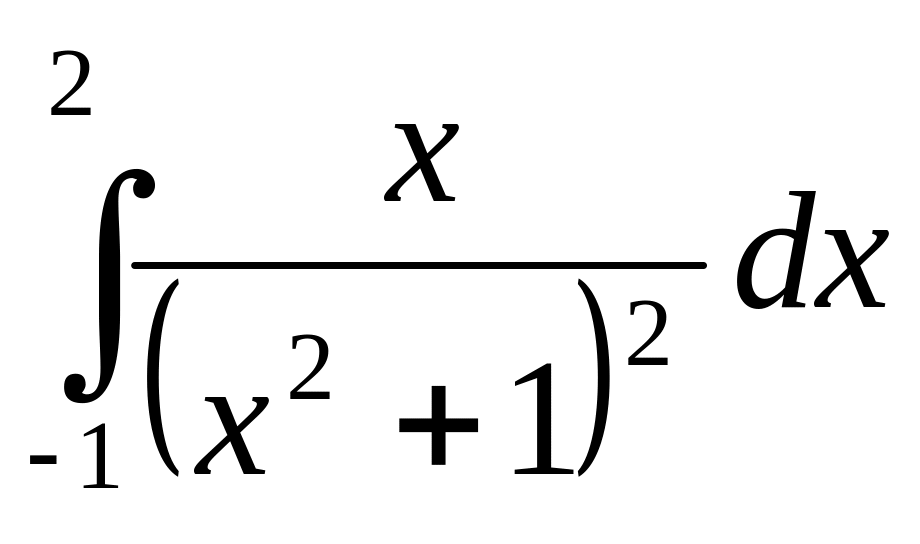- •Лабораторный практикум по информатике
- •Часть II программирование в системе турбо паскаль
- •Введение
- •Лабораторная работа №1 Создание простейшей программы
- •Начало работы с новой программой
- •Задание 1
- •Сохранение текстового файла программы на диске:
- •Задание 2
- •Задание 3
- •Задание 4
- •Лабораторная работа №2 Ввод данных и вывод результатов
- •Задания
- •Лабораторная работа №3 Программирование линейных алгоритмов
- •Задание
- •Лабораторная работа №4 Программирование разветвляющихся алгоритмов
- •Задание 1
- •Задание 2
- •Лабораторная работа № 5 Программирование циклических алгоритмов с известным числом повторений
- •Задание
- •Лабораторная работа №6 Программирование циклических алгоритмов с неизвестным числом повторений
- •Задания
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Лабораторная работа №7 Программирование алгоритмов итерационной циклической структуры
- •Задание
- •Лабораторная работа №8 Массивы
- •Лабораторная работа №9 Процедуры и функции пользователя в языке Паскаль
- •Задание
- •Лабораторная работа №10 Записи
- •Задания
- •Лабораторная работа №11 Работа с файлами
- •Лабораторная работа №12 Графический режим в языке Паскаль
- •Лабораторная работа №13 Построение графика функции
- •Задания
- •Лабораторная работа №14 Создание движущихся изображений
- •Задание 1
- •Задание 2
- •Лабораторная работа №15 Вычисление определённого интеграла численными методами
- •Метод прямоугольников
- •Метод трапеций
- •Метод Симпсона
- •Задания
- •Лабораторная работа №16 Решение нелинейных уравнений численными методами
- •Метод половинного деления
- •Метод Ньютона
- •Метод хорд
- •Задания
- •Лабораторная работа №17 Решение обыкновенных дифференциальных уравнений численными методами
- •Метод Эйлера
- •Модифицированный метод Эйлера
- •Метод Рунге-Кутта
- •Задание
- •Приложение
- •Список литературы
- •Оглавление
- •Лабораторный практикум по информатике
- •Часть II программирование в системе турбо паскаль
- •Архангельск
Метод трапеций
Сущность интегрирования методом трапеций составляет кусочно-линейная аппроксимация подынтегральной функции. Соседние точки (xi,yi) и (xi+1,yi+1), заданные таблицей в интервале axb, соединяются прямыми. Если x0=a, а xn=b, то интеграл будет представлять собой сумму площадей n трапеций высотой h каждая. На рис. 15.3 показан графически принцип метода трапеций.
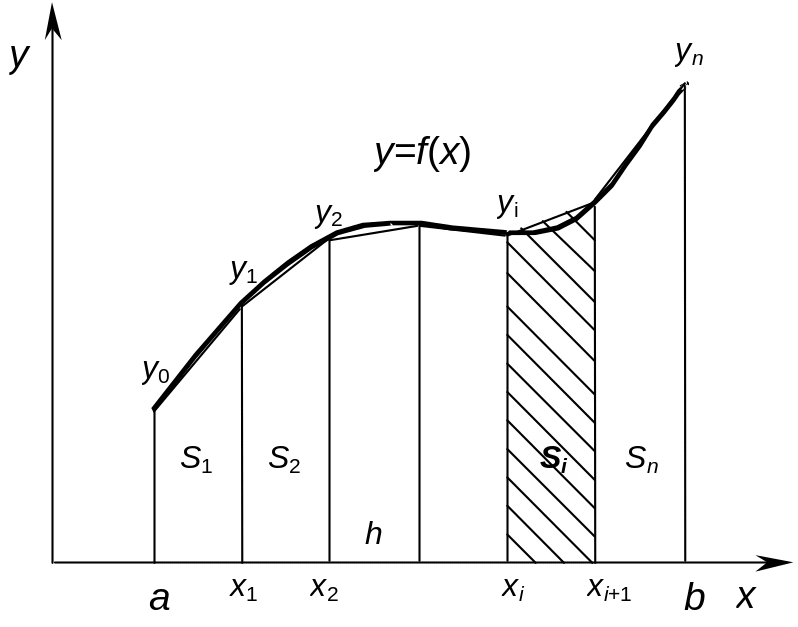
Рис.15.3. Интегрирование методом трапеций
Расчётная формула получается следующим образом:
![]()
![]()
![]()
![]()
Итоговая формула выглядит следующим образом
![]()
Таким образом, для вычисления определённого интеграла методом трапеций надо вычислить сумму значений подынтегральной функции в узлах интегрирования между a и b и умножить эту сумму на шаг интегрирования. К полученному значению прибавляется полусумма значений подынтегральной функции на концах отрезка, умноженная на шаг интегрирования. Совершенно очевидно, что чем меньше интервал h, через которые задаётся значение функции, тем с большей точностью будет вычислен определённый интеграл.
Метод Симпсона
Повысить точность результата вычисления определённого интеграла можно, если заменить линейную аппроксимацию, используемую в методе трапеций, кусочной аппроксимацией кривыми, например, параболой второго порядка. Для проведения каждой параболы требуется три точки. Аппроксимируя подынтегральную функцию параболами, получаем формулу Симпсона:
![]() ,
или
,
или
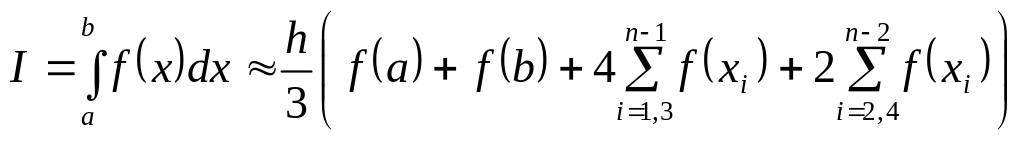 .
.
В этой формуле число интервалов должно быть чётное.
Таким образом, для вычисления определённого интеграла методом Симпсона надо вычислить отдельно суммы значений подынтегральной функции в узлах интегрирования между a и b в чётных и нечётных точках. Сумма, полученная для нечётных точек, умножается на 4, а сумма для чётных точек – на 2. К полученным двум суммам прибавляется сумма значений подынтегральной функции на концах отрезка. Полученный итог умножается на 1/3 шага интегрирования.
Все вышеприведённые алгоритмы вычисления определённого интеграла используют заданный шаг интегрирования. Кроме этого, существуют итерационные алгоритмы, в которых вычисления выполняются до заданной точности результата. При каждой итерации количество узлов интегрирования n удваивается, а затем новый результат сравнивается с результатом, полученным на предыдущем шаге. Вычисления повторяются в цикле, пока разница между результатами не станет меньше .
Задания
1. Набрать текст программы Integral1. Провести вычисления и вывести на принтер (экран) результаты расчётов при n=10; 100; 1000; 10000. Сравнить точность и скорость вычислений.
2. Сохранить под другим именем и модифицировать программу, чтобы она вычисляла значение интеграла методом трапеций. Сравнить точность и скорость вычислений при n=10; 100; 1000; 10000.
3. Сохранить под другим именем и модифицировать программу, чтобы она вычисляла значение интеграла методом парабол. Сравнить точность и скорость вычислений при n=10; 100; 1000; 10000.
4. Сохранить под другим именем и используя три предыдущих примера модифицировать программу, чтобы она последовательно вычисляла значение интеграла методом прямоугольников, трапеций и парабол. Сравнить точность и скорость вычислений при n=10; 100; 1000; 10000. Для этого результаты должны выводиться в виде таблицы:
Результаты вычисления определённого интеграла методами
n |
Прямоугольников |
Трапеций |
Парабол |
10 |
|
|
|
100 |
|
|
|
1000 |
|
|
|
10000 |
|
|
|
Варианты заданий:
№ |
Интеграл |
Точное решение |
№ |
Интеграл |
Точное решение |
1 |
|
29,25 |
5 |
|
1,84147098… |
2 |
|
0,15 |
6 |
|
1,718281828… |
3 |
|
/4 |
7 |
|
14,666(6) |
4 |
|
|
8 |
|
-1 |