27.Плотность вероятности нсв. Геометрическая интерпретация. Пример.

Ф-я 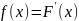наз дифференциальной ф-ё или плотностью распределения вероятностей НСВ х.

СВ х наз непрерывной, если ее ф-я распределения 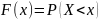непрерывна.

Плотность 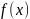должна удовлетворять двум условиям:

1. Плотность любой СВ неотрицательна

2. Интеграл от плотности п всему интервалу (а,в)=1

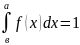
Свойства и

1. 

2. , если

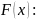
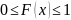
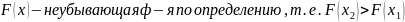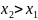
3. Если ф-я распределения непрерывна, то вероятность любого отдельного значения 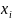СВ=0 при этом значени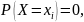и: если 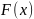- непрерывна в точке X=

4. 

5. 

6. 

7. 

8. 

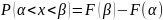
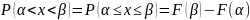
Физический смысл плотности распределения

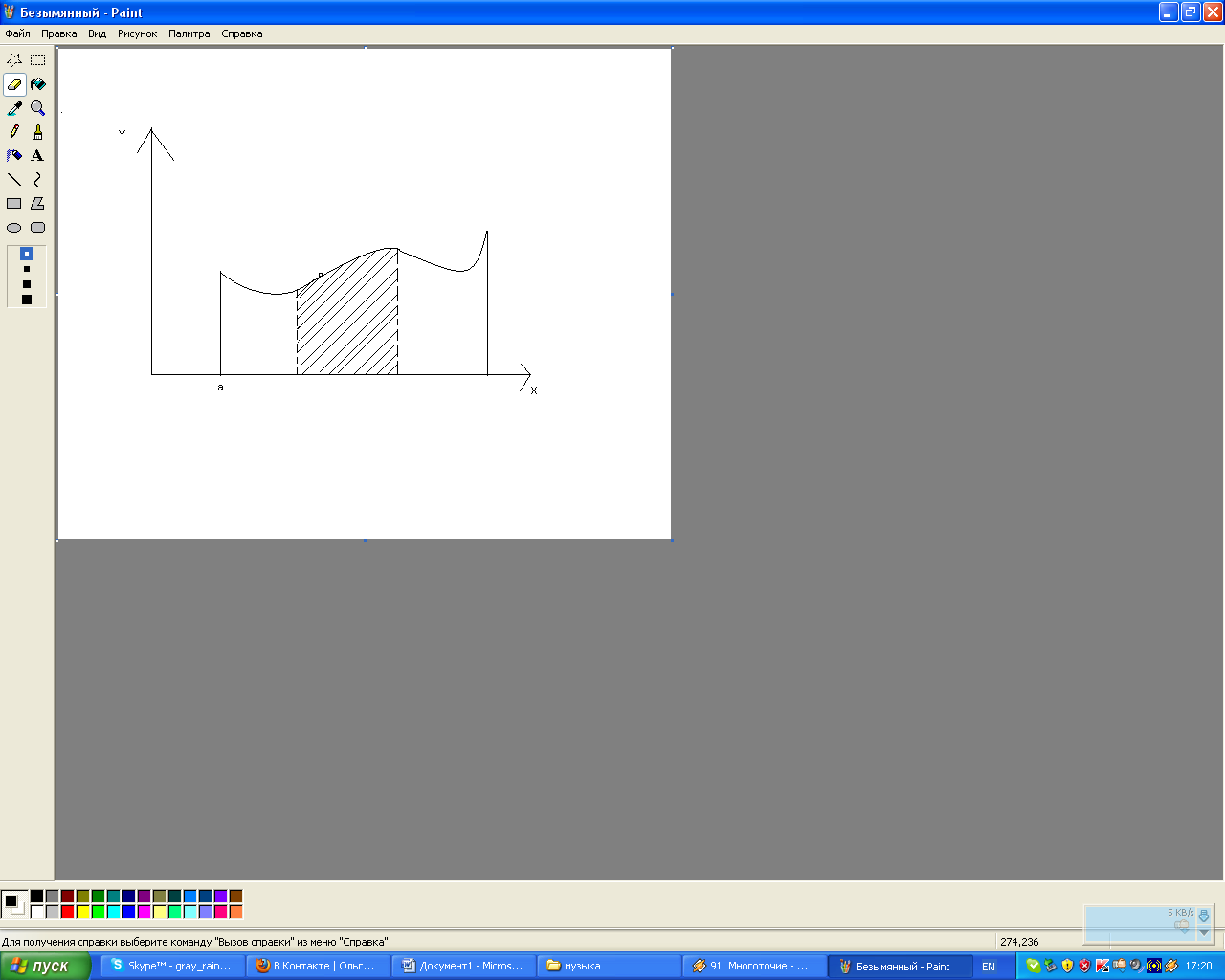
График ф-ии y=f(X) наз кривой распределения или графиком плоскости распределения. Кривая y=f(X) располагается над осью абсцисс.

28. Числовые характеристики НСВ. Пример.

1. Математическое ожидание НСВ , где -плотность вероятности

2. Дисперсия

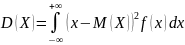
3. Среднее квадратическое отклонение

29. Дисперсия НСВ. Её свойства. Пример.

Дисперсия

Свойства:

1. D(c)=0 c=const

2. D(cx)=c²D(x)

3. D(x+y)=D(x)+D(y)

4. Размерность D(x) равна квадрату размерности СВ Х

30.Математическое ожидание НСВ. Его свойства. Пример.

Математическое ожидание НСВ , где -плотность вероятности

1. M(C)=C

2. M(CX)=CM(X)

3. M(Y+X)=M(Y)+M(X)

4. M(X*Y)=M(X)*M(Y)

5. Размерность M(X) совпадает с размерностью СВ Х

Для того чтобы оценить, как рассеяны возможные значения СВ вокруг ее М(Х) пользуются дисперсией.

31.Моменты случайной величины. Пример.

Начальным моментом q-порядка СВ наз М(х) величины x^q

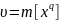
Начальным моментом q-порядка ДСВ

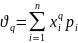
Начальным моментом q-порядка НСВ

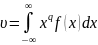
Центральным моментом q-порядка СВ наз М(х) величины

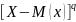
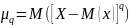
Центральным моментом ДСВ

Центральным моментом НСВ

Начальный момент первого порядка – М(х)

Центральный момент первого порядка –Д(х)

Нормированный центральный момент 3 порядка служит характеристикой скошенности или асимметрии распределения (коэффициент асимметрии)

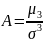
Нормированный центральный момент 4 порядка (эксцесс) служит характеристикой островершинности или плосковершинным распределением

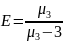
Асимметрия характеризует степень несимметричности распределения относительно его среднего.

Положительная на отклонение распред в сторону положительных значений. Отрицательный - отрицательных.

Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительное обозначает относительно остроконечное распределение, отрицательное - относительно сглаженное распределение.

32. Равномерное распределение нсв. Пример.

Непрерывная СВ Х имеет равномерное распределение на интервале [a,b], если на это интервале плотность распределения СВ пост, а вне его =0, т.е. если

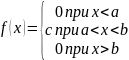, где c=const

Равномерное распределение наз законом Равномерной плотности.

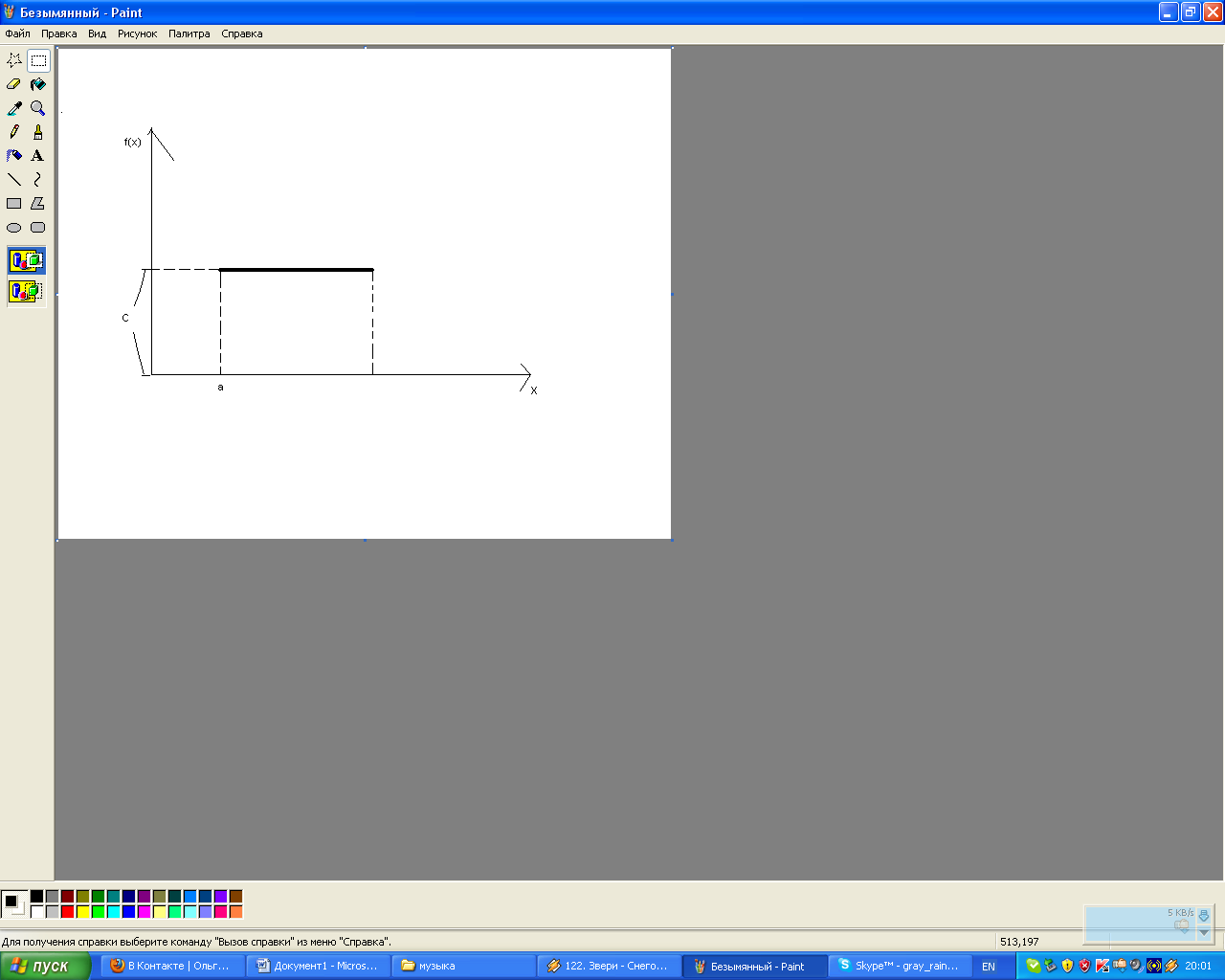
Числовые характеристики НСВ при равномерном распределении.

1. 

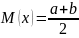
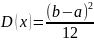2. D(x)=S²=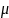

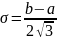
3. 

4. Коэффициент асимметрии

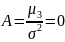
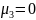
5. Четвертый центральный момент

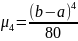
6. Коэффициент эксцесса

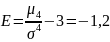
Вероятность попадания СВ Х, имеющей равномерное распределение, в интервале [α,β], который является частью участка [a,b], определяется по формуле:

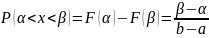
33. Нормальное распределение НСВ. Пример.

Нормальный закон распределения - явл самым распространенным из законов распределения, наиболее часто встречается в явлениях природы.

НЗР задается дифференциальной функцией

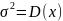
График НЗР

НЗР – называют законом Гаусса

Для расчета вероятности попадания НРСВ Х в промежуток от α до βисп формула:

, где - функция Лапласа.

34. Центральная предельная теорема (теорема Ляпунова).

Предельный закон распределения составляет предмет другой группы теорем-центральной предельной теоремы, которую иногда наз «Количественной формой закона больших чисел»

35. Закон больших чисел.

При очень большом числе случайных явлений средний их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности.

В узком смысле слова под з больших чисел понимают несколько математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения ср характеристик большого числа опытов к некоторым определенным постоянным.

36. Неравенство Чебышева.

Пусть имеется СВ х с М(х)=а и Д(х)=D. Каково бы ни было положительное число ε вероятность того что величина х отклонится от своего М(х) не меньше чем на ε ограничена сверху числом

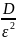
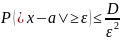
Полагаем 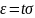, где 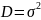, тогда неравенство можно записать в виде

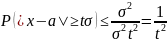
При t=1

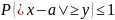
При t=2

При t=3

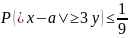
Эквивалентная форма, если перейти от события 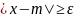к противоположному событию 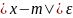, тогда получим

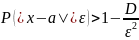
41. Числовые характеристики ВР:

1) Среднее арифметическое

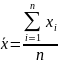
2)Средняя арифметическая взвешенная

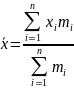
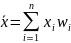
3)Дисперсия

Простая

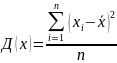
Взвешенная

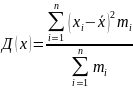
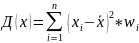
4) Среднее квадратическое отклонение

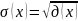
5)Коэффициент вариации

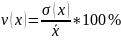
Принято считать , если коэффициент вариации больше 35%, то изучаемая статистическая совокупность является неоднородной и колеблемость признака высока.

6)Мода (Мо) ВР называется то из значений х₁, х_2, х₃, …, х_n, которому соответствует наибольшая частота.

7)Медиана-это значение варианта, которое является серединой ВР.

Пример:

С целью анализа вкладов населения в один из банков районного центра было проведено выборочное исследование 56 клиентов. Суммы вкладов внесённых клиентами в течении месяца поместили в ИВР.

Сумма вкладов	До 500	500-1000	1000-2000	2000-3000	Свыше 3000
Кол-во вкладчиков	27	11	8	8	2

А) построить кумуляту;

Б)рассчитать среднюю мощность предприятий: 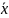- ? , х;

В) , Д(х), v(х).

Решение:

А)

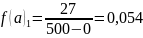
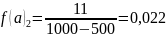
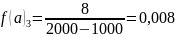
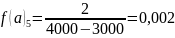
f (a)

0 ,05

0 ,04

0 ,03

0 ,02

0 ,01

500 1000 2000 3000 4000

Для того чтобы построить кумуляту, необходимо рассчитать накопленные частоты или частности.

V₁=27

V₂=27+11=38

V₂=27+11+8=46

V₄=27+11+8+8=54

V ₅=27+11+8+8+2=56

6 0

5 0

4 0

3 0

20

1 0

1 2 3 4 5

Б)Рассчитать середины интервалов:

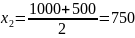
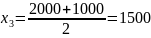
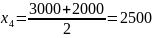
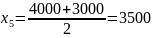
Средняя арифметическая величина

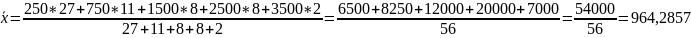
В)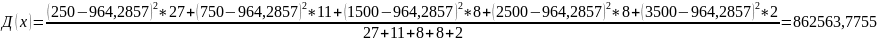

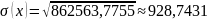
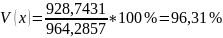
Вывод: т.к. 96,31% =>совокупность клиентов является неоднородной, в её состав вошли и крупные и мелкие вклады, что и обусловило высокую колебаемость размера вклада.