1. Элементы комбинаторики. Понятие. Пример.

Комбинаторика раздел математики, занимающийся подсчетами количества различных комбинаций между объектами.

1. Перестановка – упорядоченные множества состоящие из n различных элементов

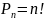
Пр-р: сколько можно составить все возможных комбинаций из букв АВСД?

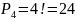
2. Перестановка с повторениями – если множество имеет повторяющиеся элементы

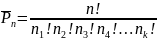
Пр-р: в слове математика: а-3, м-2, т-2, е-1, и-1, к-1

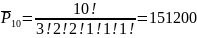
3. Размещение – упорядоченное подмножество m элементов, составленное из всего множества, содержащего n элементов

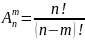
Пр-р: Сколькими способами можно распределить 3 путевки между 4мя желающими?

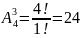
4. Размещение с повторением – случай, когда размещение из n элемениов по m элементов может содержать любой элемент сколько угодно раз от 1 до m включительно или не содержать его совсем.

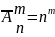
Пр-р: сколько различных двоичных чисел длинной 6 можно записать с помощью цифр 0 и 1?

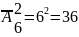
5. Сочетание из n элементов по m наз неупорядоченное подмножество, состоящее из m элементов, взятых из множества, состоящего из n элементов

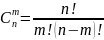
Пр-р: сколькими способами могут взойти 3 зерна пшеницы если посажено 7 зерен?

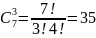
6. Сочетания с повторениями – каждое сочетание с повторением из n элементов по m элементов может содержать не только из различных элементов, но и из m каких угодно и как угодно повторяющихся элементов или не содержать совсем.

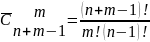
Пр-р: студент покупает 4 тет. В магазине выставлены тет 8ми видов. Сколько сущ различных способов купить 4 тет?

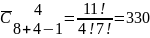
2. Правило умножения и сложения комбинаторики. Пример.

Правило суммы

Пусть элемент 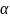можно выбрать 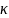способами, а элемент 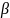- m способами, причем, если любой способ выбора отличается от любого способа выбора (независимо) то выбор «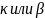 » можно сделать К+m способами.

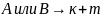
(в группе 16 юношей и 14 девушек, то преподаватель может вызвать к доске 1 учащегося 14+16=30 способами.)

Правило произведения

Если элемент можно выбрать способами, а элемент 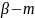способами, то пару (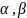 )можно выбрать _m способами. А и В

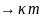
(всего 26 человек, м-21, ж -5, то 21*5=105 способов.)

3. Классическое и статистическое определение вероятности. Пример.

1. Вероятность события – это численная мера объективной возможности его появления.

Вероятность события А наз отношение числа благоприятствующих этому событию исходов к общему числу равновозможных несовместных элементарных исходов, образующие полную группу.

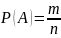, где n-число всех исходов, m-число благоприятствующих исходов.

Пр-р: вероятность выпадения решки Р(А)=m/n=1/2

2. Статистическая вероятность события принимают относительную частоту или число близкое к ней.

Под относительной частотой события понимают отношение m/n, где n-число опытов, m-число появления событий.

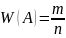
4. Геометрическое определение вероятности. Пример.

Геометрической вероятностью события наз. Отношение меры, благоприятствующей появлению события, к мере всей области.

Пр-р: на плоскости нанесена сетка квадратов со стороной 8 см. найти вероятность, что брошенный на плоскость круг радиуса не пересечет ни одной стороны квадрата.

S(А)=64см² , S(В)=36см², Р(А)=36/64=0,6=60%,

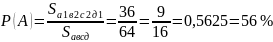
5. Свойства вероятности. Пример.

1. Вероятность случайного события А, есть положительное число, заключенное между 0 и 1

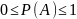
2. Вероятность достоверного события равно 1

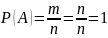
3. Вероятность невозможного события равно 0

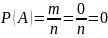
4. Сумма вероятностей 2-х противоположных событий равна 1

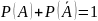
6. достоверные, невозможные и случайные события. Пример.

Достоверным событием наз событие, которое обязательно произойдет при определенном комплексе условий (омега)

Пр-р: из ящикас кубиками вытащить кубик – 100%

Невозможное – которое не может произойти в результате данного испытания

Пр-р: из ящика с зелеными кубиками вытащить красный – 0%

Случайное – которое может произойти либо не произойти в результате некоторого события.

7. виды случайных событий. Пример.

1. Совместные если в результате эксперимента наступление одного из них не исключает появление других. (при бросании монеты появление цифры на одной не иск появление цифр на других.)

2. Несовместные если появление одного исключает появление других (на экзамене не возможно получить 2 и 3 и 4 и 5)

3. Единственно возможное если в результате, испытания хотя бы одно из них обязательно произойдет (купил или не купил журнал)

4. Равновозможные события если в результате испытания ни одно из них не имеет объективно большую возможность появления чем другое (при бросании кости появл каждой грани равновозможное событие)

5. Противоположные – два единственно возможных и не совместных (попадание и промах при стрельбе)

6. Полная группа событий - совокупность всех единственно возможных и несовместных событий (получил на экзамене 5,4,3,2)