1.Предмет теории вероятностей. События.Алгебра событий. Теория вероятностей–раздел математики, изучающий закономерности случайных явлений. Разница между закономерными и случайными событиями. Закономерное событие–это событие, которое всегда осуществляется, как только создаются определённые условия. Закономерное явление – это система закономерных событий. Случайные события–это события, которые при одних и тех же условиях иногда происходят, а иногда нет. Однако случайные события подчиняются некоторым закономерностям, которые называются вероятностными закономерностями, при этом надо условится, что мы будем иметь дело не со всякими случайными событиями, а с массовыми, то есть будем предполагать, что в принципе можно создать много раз одни и те же условия, при каждом из которых могут произойти или нет некоторые случайные события. Пусть при осуществлении некоторых условий (N раз), случайное событие A, будет осуществляться N(А) раз. Число N(А) – называется частотой событий A, а отношение – относительной частотой события А.Если N велико, относительная частота для случайных массовых событий обладает свойством устойчивости. Пример: –серия испытаний. – относительная частота испытаний.   … 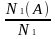

Относительная частота колеблется около определенного числа, которое характеризует данное случайное событие. Р(А) – вероятность события А.

Примеры:1)Пусть случайное событие A – выпадение герба при одном подбрасывании симметричной однородной монеты, Р(А) = 1/2 – вероятность выпадения герба.2)Статистика рождений показывает, что мальчиков рождается несколько больше, чем девочек. Доля рождения мальчиков 0,51-0,52.Р(А) = 0,51; 0,51 – вероятность рождения мальчиков. События. Достоверное событие – событие, которое всегда происходит (Ω).Невозможное событие – событие, которое не происходит никогда ().Событие Ā – событие противоположное событию A. Ā происходит тогда и только тогда, когда не происходит событие A.Суммой событий A и B называется событие A+B, которое происходит тогда и только тогда, когда происходит или A, или B, или оба вместе. Произведением событий A и B называется событие AB, которое происходит тогда и только тогда, когда происходят A и B вместе. Разностью событий A и B называется событие A-B, которое происходит тогда и только тогда, когда происходит A и не происходит B.События A и B несовместны, если AB=.Событие A влечет за собой событие B, если из наступления события A следует наступление события B (A  B).События A и B называются равносильными A=B, если выполняются одновременно два включения A=B A  B и B  A.Пример: Бросается игральная кость. A = {выпадает четное число очков} и B = {выпало число очков, не большее трех}Решение: Выпало число очков отличное от 5 (A+B).Выпало 2 (AB).Выпало число очков равное 4 или 6 (A-B).Выпадает нечетное число очков (Ā).

3.Конечное вероятностное пространство. Классическое определение вероятности. Рассмотрим случай конечного вероятностного пространства. В этом случае  состоит из конечного числа элементарных событий . = {} A – алгебра всех подмножеств  (ввиду конечности вероятностного пространства алгебра автоматически является -алгеброй), тогда вероятность P(A) для любого подмножества A задаем следующим образом. Пусть заданы неотрицательные числа P, которые удовлетворяют следующему требованию 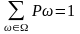, тогда вероятность события (*) (способ введения вероятности на конечном вероятностном пространстве).Очевидно, что так определенная вероятность вместе P()=0 будет удовлетворять всем аксиомам. Обозначим через - – количество элементов в множестве A. Частным случаем определения вероятности по формуле (*) будет так называемое классическое определение вероятностей, когда все P будут равны друг другу, так как ; ;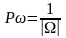 – формула классической вероятности (**)

Замечание:Модель вероятностного пространства, приводящая к классическому определению вероятностей, когда элементарные события обладают свойствами «симметрии».

Пример:Бросается кубик на стол. ₁ = {выпадает 1} ₂ = {выпадает 2} – свойства симметрии

9.Формула полной вероятности

Система событий A₁,…,A_n называется конечным разбиением(разбиением) пространства , если они:

1)попарно несовместны, т.е. A_iA_j=, если i  j.

2) A₁+A₂ +… A_n =.

Теорема (Формула полной вероятности)

Если A₁,…,A_n – разбиение и все P(A_i)>0, то для всех событий B .

Доказательство:B=B=B(A₁+…+A_n)=BA₁+…+BA_n

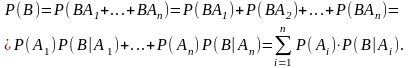
Пример. В урне находятся M-белых шаров и N-M-черных шаров. По схеме выборки без возвращения, последовательно выбираются два шара. Найти вероятность события B={второй вынутый шар белый}. A = {первый шар белый}. Ā={ первый шар черный}

Решение

A Ā =  , A + Ā = 

Пример показывает, что при правильно организованной жеребьевке шансы будут равны.

8.Условные вероятности; теорема умножения

N – число испытаний;

A, B, AB – события;

N(A), N(B), N(AB) – частоты событий;

– условная относительная частота события A при условии, что произошло событие B;

; ;

.

Если все относительные частоты событий устойчивы, тогда условная относительная частота тоже устойчива. Пусть P(B)>0.Условной вероятностью P(A|B) события A при условии, что событие B произошло, называется отношение .

P(A|B) = P_B(A) (встречается в литературе).

Теорема умножения

Если P(A)>0, P(B)>0, а P(A|B), то вероятность произведения .

Доказательство:

Доказательство следует из определения.

Пример:

1 способ. В урне находятся M-белых шаров и N-M-черных шаров. По схеме выборки без возвращения, последовательно выбираются два шара. Найти вероятность того, что оба шара будут белыми.

A = {1 вынутый шар белый} B = {2 вынутый шар белый} AB = {оба шара белых}

,

.

2 способ. .

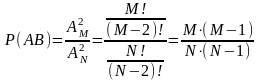Следствие.

Пусть события A₁,…,A_n таковы, что P(A₁…A_n-1 )>0 тогда .

Доказательство: Доказательство проводится методом математической индукции.

13.Функция распределения случайной величины. Её свойства. Функция распределения СВДТ. Ряд распределения может быть построен только для СВДТ, для недискретных случайных величин из-за несчетности множества возможных значений такое представление невозможно. Наиболее общей формой закона распределения пригодной для всех типов случайных величин является функция распределения. Функция F(x)=F_x(x)=P{X<x}, xR называется функцией распределения СВ Х. С помощью функции распределения можно выразить вероятности попадания CB Х в различные интервалы вида x₁X< x₂ , x₁X x₂ , x₁<X x₂ , x₁<X< x₂ . Пусть x₁ < x₂ , тогда {X< x₂} разложим в сумму двух несовместных событий {X<x₂}={X< x₁}+{ x₁ X<x₂}, тогда P{X<x₂}=P({X< x₁} +{ x₁ X<x₂})=P{X< x₁}+

P{ x₁ X<x₂}; F_X(x₂)=F_X(x₁)+ P{ x₁Xx₂};P{ x₁Xx₂}= F_X(x₂)-F_X(x₁) (**) Событие {X>x} можно представить, как счетную сумму несовместных событий Согласно (**).

P{X>x}=1- F_X(x+0); P{Xx}=1- P{X>x}=F_X(x+0);

P{x₁Xx₂}=F_X(x₂+0)- F_X(x₁); P{ x₁Xx₂}=F_X(x₂+0)- F_X(x₁+0);P{ x₁Xx₂}=F_X(x₂)- F_X(x₁+0);

P{ X=x}=F_X(x+0)- F_X(x);

Теорема.

Функция F_X(x) обладает следующими свойствами:

1. F_X(x) – не убывает;

2. F_X(x) – непрерывна слева;

3. F_X(+)=1;

4. F_X(-)=0;.

Доказательство 3 и 4:

1.Следует из (**), т.к. P{x₁Xx₂ }0.

2.Следует из аксиомы непрерывности 4, т.к. события

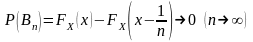
F_X(x)= F_X(x-0) .

Свойства 3, 4 вытекают из аксиомы счетной аддитивности (3*), т.к. =ΣA_n (-<n<), где

A_n={ n-1X()<n}, тогда

Пусть (по теореме Вейeрштрасса).

(0 F_X(N)  1 )

Из равенства P{X=x}=F_X(x+0)-F_X(x) следует, что в точках разрыва функции F_X(x) имеет место положительная вероятность. P{X=x}>0

Так как при каждом натуральном n может быть не более n-точек x с вероятностями P{X=x}1/n, то у функции F_X(x) имеется не более счетного числа точек разрыва.Обозначим через x₁,x₂,.. все точки разрыва функции F_X(x), если вероятности P{X=x}=P_k таковы, что Σp_k=1, то это равносильно тому, что СВ X имеет дискретное распределение, то есть является СВДТ.Замечание. Для СВДТ F_X(x) имеет ступенчатый вид. Пример.

X -3 -1 0 2 3

P 0,1 0,3 0,1 0,3 0,2

Получить функцию распределения и построить ее график. Решение. F_X(x)=P{X<x}, т.е. F_X(x)=0(x-3); F_X(x)=0,1(-3<x-1); F_X(x)=0,4(-1<x0);

F_X(x)=0,5(0<x2); F_X(x)=0,8(2<x3); F_X(x)=1(x>3);

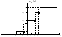
P{X=2}= F_X(2+0)- F_X(2)=0,8-0,5=0,3;

P{-1<X2}=F_X(2+0)-F_X(-1+0)=0,8-0,4=0,4 Введем новое важное понятие индикатора события.

Опр:Индикатором события A  A называется СВ : .

Ряд распределения случайной величины I_A имеет следующий вид

I_A 0 1

P 1–p p

где р-вероятность события А.