Вопрос 6.3. Формула Грина и ее приложения.

Определение 6.2. Гладкая или кусочно-гладкая замкнутая кривая Г называется контуром.

Конец определения.

Определение 6.3. Контур называется простым, если он не имеет самопересечений и любая прямая, параллельная осям координат, пересекает его не более чем в двух точках.

Конец определения.

Теорема 6.1. Пусть плоская область D, ограничена простым контуром Г и пусть на области D заданы две непрерывных функции и с непрерывными частными производными первого порядка. Тогда справедлива формула Грина

где ‑ контур, обходимый против часовой стрелки.

Доказательство. Из условия теоремы следует существование двух функций , графики которых ограничивают область D (см. рис. 2) и образуют кривые и соответственно. Тогда справедлива цепочка равенств

Из условия теоремы так же следует, что существуют функции , которые ограничивают область D слева и справа и графики которых образуют кривые и соответственно. Тогда

Рис. 6.2. К доказательству формулы Грина.

Тогда для полного интеграла 2-го рода получим

Конец доказательства.

Замечание 6.1. Формула Грина справедлива для любого кусочно-гладкого контура без самопересечений, который можно разбить на простые контуры.

Следствие 6.1. Площадь плоской области D равна , где Г ‑ контур, ограничивающий область D.

Доказательство. Воспользуемся формулой Грина

.

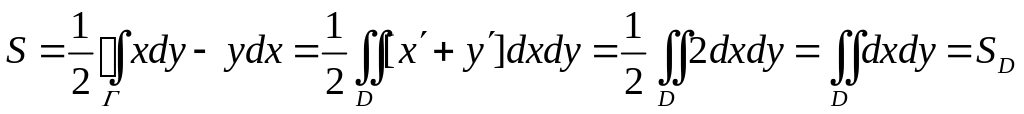Конец доказательства.

Следствие 6.2. Пусть на области D и частные производные непрерывны. Тогда для любого контура Г, лежащего в области D

. (1)

Замечание 6.2. Несложно доказать и обратное утверждение о том, что если для любого замкнутого контура Г в области D интеграл (1) равен 0. то .

Конец примера.

Лекция № 7. Поверхностные интегралы.

Вопрос 7.1. Определение гладкой поверхности. Ориентация и нормаль.

Определение 7.1. Множество точек пространства, координаты которых удовлетворяют уравнению , называется поверхностью.

Конец определения.

Определение 7.2. Поверхность S, заданная уравнением , называется гладкой, если функция является непрерывно дифференцируемой и

.

Пример 7.1. Сфера единичного радиуса является гладкой поверхностью, так как

Конец примера.

Определение 7.3. Поверхность S называется кусочно-гладкой, если она состоит из гладких кусков, разделенных кусочно-гладкими кривыми.

Конец определения.

Пример 7.2. Примером кусочно-гладкой поверхностью является куб, состоящий из 8-ми гладких кусков.

Конец примера.

Определение 7.4. Окрестностью точки M поверхности S называется множество точек пересечения открытого шара с центром в точке M с поверхностью.

Конец определения.

Из определения поверхности следует, что в каждой точке M гладкой поверхности существует касательная плоскость

,

коэффициенты которой непрерывны как функции точек поверхности в некоторой окрестности точки M. Вектор

перпендикулярен касательной плоскости поверхности.

Определение 7.5. Нормалью к поверхности S в точке M называется вектор единичной длины, перпендикулярный касательной плоскости. Нормаль также называется нормальным вектором.

Конец определения.

Из определения гладкой поверхности S следует, что в каждой точке она имеет нормаль

.

Ясно, что в каждой точке гладкой поверхности существует ровно две противоположно направленные нормали .

Определение 7.6. Полем нормалей называется правило или закон, по которому каждой точке поверхности ставится в соответствие нормальный вектор.

Конец определения.

Из определения следует, что любая гладкая поверхность S имеет поле нормалей и причем не одно. Естественно рассматривать только те поля нормалей для гладких поверхностей, которые являются непрерывными функциями точек поверхности S. Это означает, что при непрерывном переносе нормали вдоль любого замкнутого контура на поверхности S, не пересекающем края поверхности, нормаль возвращается в прежнее положение.

Определение 7.7. Поверхность S называется ориентируемой или двусторонней, если на ней существует непрерывное поле нормалей.

Конец определения.

Если поверхность ориентируемая (см. рис. 1), то она имеет два непрерывных поля нормалей, направленных в противоположные стороны. Одно из этих полей задает верхнюю сторону поверхности, другое нижнюю. Если поверхность задана функцией , то в этом случае естественно считать внешней стороной ту, нормаль которой образует острый угол с ось Z. Если ориентируемая поверхность замкнута, то внешней стороной считают ту, нормаль которой направлена во внешнюю часть пространства. Соответственно, внутренняя сторона имеет нормаль, направленную во внутреннюю часть пространства, ограниченную поверхностью.

Примером неориентируемой поверхности является знаменитый лист Мебиуса (см. рис. 7.1)

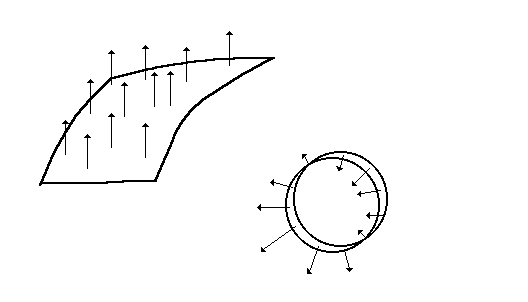
Рис 7.1. Ориентируемая и неориентируемые поверхности.