2) Сферические координаты

Вычислим их якобиан

.

Разложим последний определитель по третьему столбцу

Рис. 4.2. Сферическая система координат.

Сферические координаты удобно использовать, если область интегрирования является шаром или частью шара. Тогда в сферических координатах область интегрирования будет прямоугольным параллелепипедом.

Пример 4.2. Вычислить объем эллипсоида .

.

Перейдем в сферическую систему координат

Вопрос 4.2. Геометрические и физические приложения тройного интеграла.

1) Вычисление объемов тел .

2) Масса тела с плотностью .

3) Заряд тела с плотностью заряда . Лекция n 5. Криволтнейные интегралы.

Вопрос 5.1. Криволинейный интеграл 1-го рода.

Определение 5.1. Кривая Г называется гладкой кривой, заданной параметрически на плоскости, если она определяется уравнениями

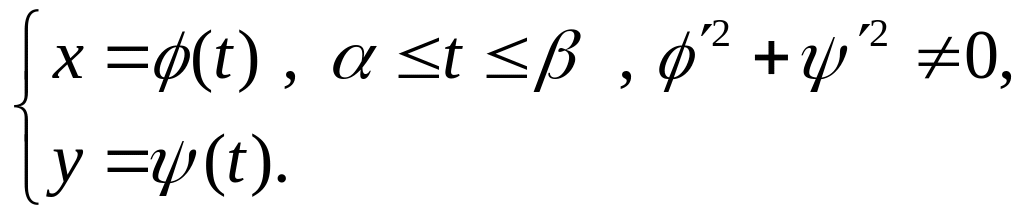
где ‑ непрерывные на функции, имеющие непрерывные производные .

Если , то кривая называется замкнутой.

Конец определения.

Замечание 5.1. Из неравенства следует, что в любой точке отрезка или , или . Если , то для функции существует обратная функция . Поэтому существует функция . Если , то аналогично . Таким образом, гладкую кривую в окрестности любой точки можно представить функцией или .

Пример 5.1. Окружность ‑ гладкая замкнутая кривая

Конец примера.

Определение 5.2. Кривая Г называется ориентированной, если указаны ее начало и конец и положительному направлению обхода (то есть от начала к концу) соответствует изменение t от наименьшего значения к наибольшему.

Конец определения.

Пример 5.2. Окружность ориентирована положительно:

.

Конец примера.

Определение 5.3. Кривая Г называется кусочно-гладкой, если ее можно разбить на конечное число частей, каждая из которых есть гладкая кривая.

Конец определения.

Определение 5.4. Пусть на кусочно-гладкой кривой задана непрерывная функция . Разобьем кривую на n частей с длинами и на каждой возьмем произвольным образом точку . Тогда сумма

называется интегральной суммой криволинейного интеграла I-го рода.

Конец определения.

Замечание 5.2. Кусочно-гладкая кривая всегда спрямляема, поэтому можно определить длину любой ее части.

Определение 5.5. Пусть . Тогда криволинейный интеграл первого рода от функции по кривой Г определяется как предел интегральных сумм

,

если он не зависит от выбора промежуточных точек и способа разбиения кривой на части.

Конец определения.

Рис. 5.1. К определению криволинейного интеграла 1-го рода.

Вопрос 5.2. Вычисление криволинейного интеграла 1-го рода через определенный интеграл.

Пусть плоская кривая Г задана параметрическими уравнениями

Разобьем отрезок на n частей точками .

Тогда плоская кривая Г будет так же разбита на n частей точками

,

координаты которых, соответственно, равны

.

Длина каждой части разбиения равна

.

Составим интегральную сумму

.

Преобразуем интеграл по теореме о среднем, тогда получим

Можно показать, что при

Таким образом, при переходе к параметрическим уравнениям кривой, криволинейный интеграл 1-го рода сводится к определенному интегралу

.

Если кривая Г задана функцией на отрезке , то ее параметрические уравнения примут вид

тогда

Если Г ‑ кривая в пространстве, заданная параметрическими уравнениями

то криволинейный интеграл 1‑го рода сводится так же к определенному интегралу

.

Пример 5.3. Вычислить интеграл по окружности от функции при обходе окружности против часовой стрелки.

Параметрические уравнения окружности , поэтому .

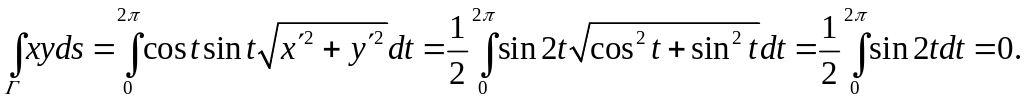Конец примера.

Пример 5.4. Вычислить криволинейный интеграл 1-го рода от функции по кривой Г:

Конец примера.