Вопрос 3.2. Вычисление тройного интеграла через повторные интегралы.

Пусть функция задана на прямоугольном параллелепипеде

,

тогда повторными интегралами называются интегралы вида:

Теорема 3.1.(Фубини). Если функция непрерывна на Q, то справедлива цепочка равенств

Эта теорема приводится без доказательства. Она дает практический способ вычисления тройного интеграла.

Пример 3.1.

.

Конец примера.

Вопрос 3.3. Тройные интегралы для произвольных областей.

Пусть M есть произвольная область в пространстве (см. рис. 2) Пусть Q прямоугольный параллелепипед, содержащий область M. Определим функцию

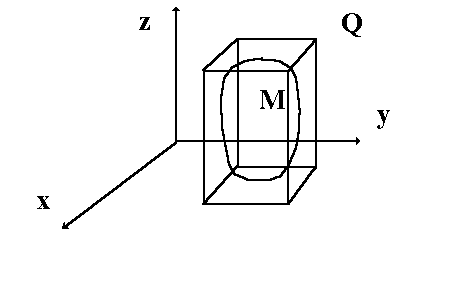
Рис. 2 Тройной интеграл по произвольному множеству.

Тогда по определению интегралом от функции по множеству M называется интеграл

Если существует интеграл , то число V(M) называется объемом области M, а область M называется измеримой. Справедлива теорема:

Теорема 3.2. Если ограниченная, замкнутая область M имеет кусочно-гладкую границу, то она измерима и любая кусочно-непрерывная функция интегрируема на области M.

Для тройных интегралов справедливы следующие свойства (в добавление к свойствам 3.1 – 3.8, где нужно заменить Q на M):

1) , если M кусочно-гладкая поверхность.

2) , если пересечение и пусто или есть кусочно-гладкая поверхность.

3) Обобщенная теорема Фубини. Пусть М есть цилиндр и D его проекция. Пусть цилиндр M ограничен графиками непрерывных функций , тогда существуют тройной и повторный интегралы и они равны (см. рис. 3)

.

Доказательство. Пусть Q прямоугольный параллелепипед, содержащий M (см. рис.3), тогда по определению

где учтено, что , если точка не принадлежит M.

Конец доказательства.

Рис. 3. К доказательству обобщенной теоремы Фубини.

Пример 3.2. Вычислить интеграл от функции по множеству (см. рис. 4)

Рис. 4. К примеру 3.2.

.

Конец примера.

Лекция № 4. Тройные интегралы.

Вопрос 4.1. Замена переменных в тройном интеграле.

Пусть D множество точек и сделана замена переменных

где пробегает некоторое множество M, тогда если функции , и непрерывно дифференцируемы, и каждой тройке соответствует только одна тройка , то справедлива формула замены переменных в тройном интеграле

где

‑ якобиан отображения.

Замечание 4.1. Формулы , , называются отображением. Отображение, о котором речь шла выше, называется непрерывно дифференцируемым и взаимно однозначным.

Замечание 4.2. Если отображение , , взаимно однозначно и непрерывно дифференцируемо, то его якобиан .

Рассмотрим замену переменных в различных системах координат.

1) Цилиндрическая система координат (см. рис. 1)

Вычислим ее якобиан :

Рис. 4.1. Цилиндрическая система координат.

Тогда формула замены переменных в цилиндрической системе координат имеет вид

Замечание 4.3. Цилиндрические координаты удобно использовать, если область интегрирования представляет собой цилиндр или его часть. Тогда в цилиндрической системе координат область интегрирования будет прямоугольным параллелепипедом.

Пример 4.1. Вычислить интеграл .

Область интегрирования есть цилиндр радиуса 2. Поэтому перейдем в цилиндрическую систему координат

область изменения  находится из неравенства

Область изменения координаты  не зависит от координаты , поэтому в цилиндрической системе координат получаем в качестве области интегрирования прямоугольный параллелепипед .

Конец примера.