2) Обобщенные полярные координаты:

Вычислим ее якобиан

.

Обобщенные полярные координаты удобно использовать, если область интегрирования является эллипсом или эллиптическим сектором, эллиптическим кольцом или его частью. Тогда в обобщенных полярных координатах область интегрирования будет прямоугольником.

Пример 2.2. Вычислить площадь эллипса

Конец примера.

Вопрос 2.2. Геометрические и физические приложения двойного интеграла.

1) вычисление площадей плоских фигур

;

2) объем цилиндра, ограниченного графиком функции

;

3) площадь поверхности, заданной графиком функции и определенной на множестве D.

Поясним, откуда взялась эта формула. Во-первых, дадим определение площади поверхности.

Определение 2.1. Пусть дана поверхность S, заданная графиком непрерывно дифференцируемой функции , определенной на области изменения переменных . Разобьем поверхность S на части кусочно-гладкими кривыми. На каждой части выберем произвольным образом точку и проведем через нее касательную плоскость. С проектируем каждый участок поверхности на свою касательную плоскость. Пусть i-я проекция имеет площадь . Назовем диаметром разбиения d наибольший линейный размер части разбиения. Составим сумму . Предел этой суммы при стремлении диаметра разбиения к 0, если он не зависит от способа разбиения и выбора промежуточных точек, называется площадью поверхности S.

Конец определения.

Рассмотрим для простоты прямоугольную область D. Разобьем ее на прямоугольники размером . Каждому такому прямоугольнику соответствует некоторая часть поверхности (см. рис. 2). Проекция этой части приближенно равна параллелограмму, построенному на векторах . Тогда площадь проекции выбранного участка приближенно равна площади параллелограмма, построенного на векторах .

.

Раскладывая определитель по первой строке, получим

.

Суммируя по i и j получим интегральную сумму двойного интеграла и переходя к пределу, получи рассматриваемую формулу

.

4) масса плоского тела с плотностью

.

5) заряд плоского тела с плотностью заряда

.

Лекция № 3. Тройные интегралы.

Вопрос 3.1. Тройные интегралы на прямоугольных параллелепипедах и их свойства.

Пусть функция задана на прямоугольном параллелепипеде

Рис. 1 Разбиение прямоугольного параллелепипеда Q.

Разобьем отрезки и точками

,

и проведем через точки разбиения плоскости, параллельные соответствующим координатным плоскостям. Тогда прямоугольный параллелепипед Q будет разбит на lmn прямоугольных параллелепипедов разбиения. Возьмем один из них

.

Под его диаметром будем понимать диагональ длиной

Определение 3.1. Диаметром разбиения T прямоугольного параллелепипеда Q называется максимальный диаметр прямоугольных параллелепипедов разбиения

На каждом параллелепипеде разбиения выберем некоторую точку . Тогда интегральной суммой функции называется величина

где ‑ объем прямоугольного параллелепипеда разбиения .

Определение 3.2. Тройным интегралом от функции на прямоугольном параллелепипеде Q называется число I, равное пределу интегральных сумм при стремлении диаметра разбиения к 0, если этот предел не зависит от выбора точек .

Конец определения.

Тройной (трехкратный) интеграл по прямоугольному параллелепипеду Q обозначается символом

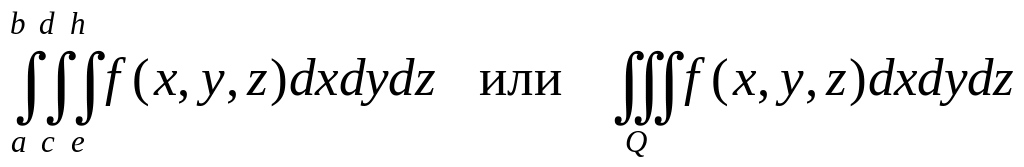
Свойства тройного интеграла:

Свойство 3.1. Если функция интегрируема на прямоугольнике Q, то она ограничена (так же как для определенных интегралов).

Свойство 3.2. Если функция кусочно-непрерывна, то она интегрируема.

Свойство 3.3.  (объем прямоугольного параллелепипеда Q).

Свойство 3.4.

Свойство 3.5.

.

Эти два свойства выражают линейность тройного интеграла. Их справедливость непосредственно следует из линейности интегральных сумм и линейности предельного перехода.

Свойство 3.6. Если функция , то .

Это свойство положительной определенности тройного интеграла.

Свойство 3.7. Если функция ‑ непрерывна, то существует такая точка P из прямоугольного параллелепипеда Q, что

,

где объем прямоугольного параллелепипеда.

Это свойство носит название теоремы о среднем значении.

Свойство 3.8. Если прямоугольный параллелепипед Q есть (объединение двух прямоугольных параллелепипедов, пересекающихся только по границе), то

Это свойство носит название аддитивности тройного интеграла.