Лекция № 13. Функциональные ряды.
Вопрос 13.1. Функциональные ряды. Поточечная и равномерная сходимость.
Определение
13.1.
Функциональным рядом называется ряд
вида
,
члены которого являются функциями,
заданными на одном и том же множестве
M.
Конец определения.
Определение 13.2. Функциональный ряд сходится в точке x, если при подстановке этого значения x в аргумент членов ряда, он сходится как числовой ряд.
Конец определения.
Определение 13.3. Функциональный ряд сходится в точке x абсолютно, если при подстановке этого значения x в аргумент членов ряда, он сходится абсолютно как числовой ряд
Конец определения.
Определение 13.4. Функциональный ряд сходится по точечно (или просто сходится) на множестве M, если он сходится в каждой точке этого множества.
Конец определения.
Определение 13.5. Функциональный ряд сходится абсолютно на множестве M, если он сходится абсолютно в каждой точке этого множества.
Конец определения.
По точечной сходимости не достаточно, чтобы сумма ряда была бы непрерывной, интегрируемой или дифференцируемой функцией, если такими являются ее члены. В связи с этим вводят равномерную сходимость функционального ряда.
Определение
13.6.
Функциональный ряд сходится равномерно
на множестве M,
если для любого
существует такое
,
что для всех
выполнено неравенство
,
где
‑ сумма ряда,
‑ частичная сумма ряда.
Конец определения.
Согласно этому определению, N-я частичная сумма отличается от суммы равномерно сходящегося ряда не более чем на величину e сразу для всех значений x и всех . В то время как при поточечной сходимости величина e зависит от x. Приведем признак равномерной сходимости функционального ряда.
Теорема
13.1. (Признак Вейерштрасса).
Пусть функциональный ряд сходится
поточечно на некотором множестве. Если,
начиная с некоторого натурального
числа N,
все члены ряд удовлетворяют неравенству
и числовой ряд
сходится, то функциональный ряд сходится
абсолютно и равномерно на этом множестве.
Доказательство.
Из неравенства
следует, что функциональный ряд сходится
абсолютно на данном множестве. Обозначим
его сумму через функцию
.
Тогда
и, последовательно, получаем
,
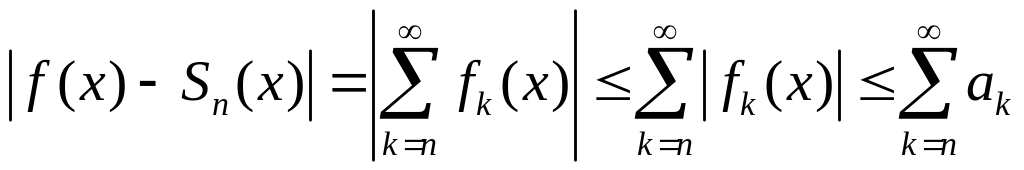но у числового сходящегося ряда для
любого
существует такое
,
что для всех
выполнено неравенство
.
Следовательно, и для функционального
ряда
для всех
независимо от x.
Конец доказательства.
Пример
13.1. Ряд
сходится равномерно по признаку
Вейерштрасса, так как этот ряд можно
мажорировать числовым рядом
,
который сходится. Действительно
.
Конец примера.
Вопрос 13.2. Непрерывность, интегрируемость и дифференцируемость суммы равномерно сходящихся рядов.
Теорема 13.2. Если функциональный ряд сходится равномерно и его члены являются непрерывными функциями на некотором множестве, то его сумма является непрерывной функцией на том же самом множестве, то есть
.
Доказательство. Пусть есть сумма функционального ряда. Рассмотрим разность
Здесь
‑ n-я
частичная сумма функционального ряда.
В силу равномерной сходимости ряда
можно для любого
выбрать
,
такое, что
для всех
и всех x
из данного множества. В силу непрерывности
членов функционального ряда для любого
можно указать такое
,
что для всех
удовлетворяющих неравенству
выполнено неравенство
.
Таким образом, получаем, что
как только
.
То есть сумма ряда непрерывна в точке
x.
Отсюда в силу произвольности x
следует непрерывность суммы функционального
ряда
Конец доказательства.
Пример 13.2. Ряд
сходится равномерно по признаку
Вейерштрасса на вещественной оси x,
так как его можно мажорировать сходящимся
числовым рядом
.
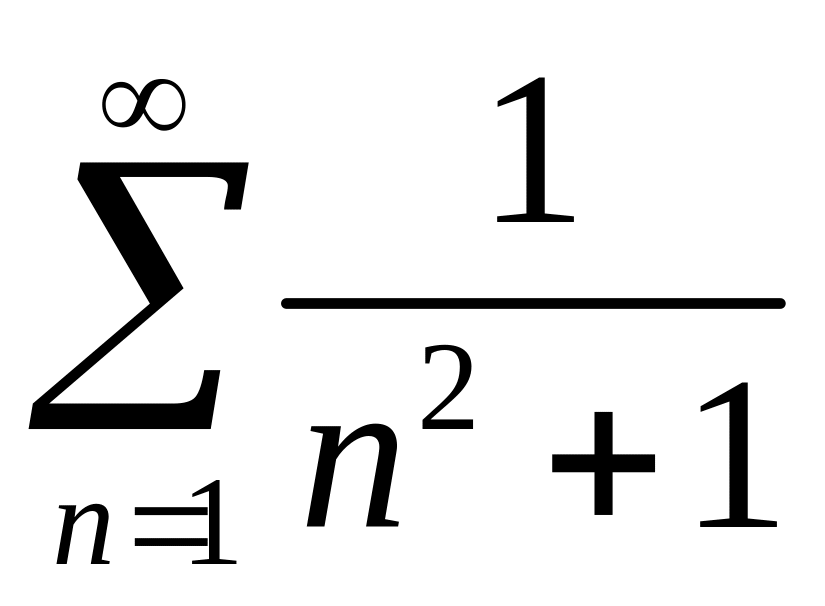Так как члены функционального ряда
непрерывны, то сумма данного числового
ряда непрерывна для любого x.
Конец примера.
Теорема 13.3. Если функциональный ряд сходится равномерно и его члены являются непрерывными функциями на некотором множестве, то его сумма является интегрируемой функцией на том же самом множестве, то есть
.
Доказательство.
Пусть
есть сумма функционального ряда. Так
как члены ряда непрерывны на отрезке
,
то в силу равномерной сходимости функция
тоже непрерывна на этом отрезке. Тогда
функция
интегрируема на
.
Для произвольного
существует
такое, что для всех
выполнено неравенство
.
Отсюда, интегрируя, получим для всех
:
,
то есть ряд из интегралов сходится к требуемой сумме.
Конец доказательства.
Пример 13.3. Возьмем ряд из примера 13.2. Так как он сходится равномерно и состоит из непрерывных функций, то его можно почленно интегрировать, тогда
.
Конец примера.
Замечание 13.1. Если верхний предел интегрирования будет переменным, то несложно доказать, что ряд из интегралов будет на конечном отрезке сходится равномерно.
Теорема 13.4. Пусть функциональный ряд сходится на отрезке и его члены являются непрерывно дифференцируемыми функциями на этом отрезке. Тогда, если ряд из производных сходится равномерно на отрезке , то ряд можно дифференцировать почленно, и справедлива формула
.
Доказательство. Так как члены ряда из производных являются непрерывными функциями, и ряд сходится равномерно на отрезке , то его сумма является интегрируемой функцией на том же самом множестве, то есть
.
Дифференцируя это равенство, получим
Что и требовалось доказать.
Конец доказательства.
Пример
13.4. Пусть
дан ряд
.
Используя признак Вейерштрасса можно
легко доказать равномерную сходимость
ряда из производных
.
Тогда по теореме 13.4 получим
.
Конец примера.