Лекция № 11. Числовые ряды.

Вопрос 11.1. Бесконечные числовые ряды. Сходимость. Сумма числового ряда.

Определение 11.1. Бесконечным числовым рядом называется формальная бесконечная сумма чисел

Конец определения.

Числовой ряд так же можно записать в сокращенном виде . Числа называются членами ряда. Величина называется n-м членом ряда и является функцией натурального параметра .

Определение 11.2. Если все члены ряда имеют одинаковый знак, то ряд называется знакопостоянным. В противном случае ряд называется знакопеременным. В частности, если знаки членов ряда чередуются, то ряд называют знакочередующимся.

Конец определения.

Определение 11.3. Сумма первых n членов ряда называется n-й частичной суммой

.

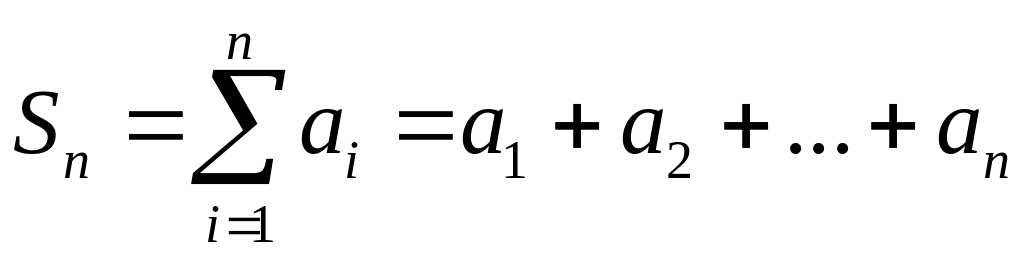Конец определения.

Определение 11.3. Числовой ряд называется сходящимся, если существует конечный предел его частичных сумм. Величина этого предела называется суммой числового ряда. Если не существует конечного предела частичных сумм, то ряд называется расходящимся.

Конец определения.

Если ‑ сумма сходящегося ряда, то будем писать .

Пример 11.1. Бесконечная геометрическая прогрессия

Вычислим n-ю частичную сумму , тогда получим

Таким образом - условие сходимости геометрической прогрессии, ‑ условие расходимости геометрической прогрессии.

Конец примера.

Пример 11.2. Вычислить сумму ряда .

Так как 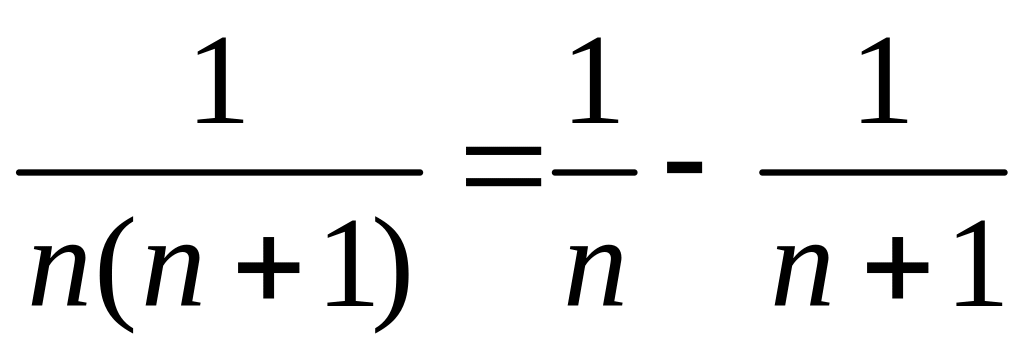, то

.

Отсюда .

Конец примера.

Вопрос 11.2. Свойства сходящихся рядов.

Свойство 11.1. При сложении двух сходящихся рядов получается сходящийся ряд, сумма которого равна сумме сумм этих рядов.

.

Доказательство. Обозначим n-е частичные суммы этих рядов через соответственно. Тогда и переходя к пределу, получим

.

Конец доказательства.

Замечание 11.1. При сложении двух расходящихся рядов может получиться как сходящийся, так и расходящийся ряд. Если члены рядов знакопостоянны и одного знака, то сумма двух расходящихся рядов есть расходящийся ряд.

Свойство 11.2. При вычитании двух сходящихся рядов получается сходящийся ряд, сумма которого равна разности сумм этих рядов

.

Доказательство. Обозначим n-е частичные суммы этих рядов через соответственно. Тогда и, переходя к пределу, получим

.

Конец доказательства.

замечание 11.2. При вычитании двух расходящихся знакопостоянных рядов одного знака может получиться как сходящийся, так и расходящийся ряд.

Свойство 11.3. При умножении сходящегося ряда на число получается сходящийся ряд, сумма которого равна произведению суммы исходного ряда на это число

.

Доказательство. Обозначим n-е частичные суммы этих рядов через и соответственно. Тогда и переходя к пределу, получим .

Конец доказательства.

Замечание 11.3. При умножении расходящегося ряда на число вновь получается расходящийся ряд.

Свойство 11.4. Если у числового ряда отбросить первые k членов, то его сходимость не нарушится, а сумма уменьшится на сумму первых k членов.

Доказательство. Частичные суммы этих рядов связаны соотношением

.

Тогда переходя к пределу, получим

,

или

.

Конец доказательства.

Замечание 11.4. Из доказательства свойства 11.4 следует, что если ряд расходится, то и после отбрасывания первых k членов ряда, ряд будет расходиться.

Свойство 11.5. (Необходимый признак сходимости). Если ряд сходится, то его n-й член стремиться к нулю с ростом n до бесконечности, то есть при .

Доказательство. Пусть n-я частичная сумма ряда есть . Тогда . Поэтому, если ряд сходится, то , отсюда следует, что или .

Конец доказательства.

Замечание 11.5. Из свойства 11.5 следует, что если предел n-го члена ряда не равен 0 или не существует при n®¥, то ряд расходится.

Замечание 11.6. Если , то ряд может, как сходится, так и расходится.

Пример 11.3. , так как , то ряд расходится.

Конец примера.

Пример 11.4. Гармонический ряд , , но этот ряд расходится. Действительно, . Если ряд сходится, то . Тогда , что противоречит неравенству . Следовательно, ряд сходится.

Конец примера.