Лекция № 8. Поверхностные интегралы.

Вопрос 8.1. Поверхностные интегралы 2-го рода.

Пусть S ‑ кусочно-гладкая поверхность, в каждой точке M которой задан вектор . Напомним, что в этом случае говорят, что на S задано векторное поле. Это векторное поле можно разложить по базису

.

Если известны координаты точки , то это же соотношение можно записать в виде

.

Если три функции P(M), Q(M), R(M) - непрерывны на поверхности S, то векторное поле называется непрерывным на S.

Пусть поверхность S к тому же ориентируема, то есть на ней существует непрерывное векторное поле нормалей , тогда скалярное произведение непрерывно. Поэтому существует поверхностный интеграл первого рода

Определение 8.1. Указанный интеграл называется полным поверхностным интегралом 2-го рода или потоком векторного поля через поверхность S в направлении нормали .

Конец определения.

Рассмотрим свойства этого интеграла:

1) при изменении ориентации поверхности на противоположную знак интеграла меняется на противоположный.

Действительно, так как при изменении ориентации поверхности на противоположную меняется на , то знак интеграла также меняется на противоположный.

2) линейность поверхностного интеграла 2-го рода

3) Аддитивность поверхностного интеграла 2-го рода. Если S ‑ поверхность, разделенная кусочно-гладкой кривой на части и , то

.

Вопрос 8.2. Вычисление поверхностного интеграла через двойной интеграл.

Пусть S гладкая поверхность, которая однозначно проектируемая на три координатные плоскости. Это означает, что любая прямая, параллельная одной из координатных осей, пересекает поверхность не более, чем в одной точке. Обозначим проекции поверхности S на три координатные плоскости через (см. рис. 1).

Рис. 8.1. К вычислению поверхностного интеграла 2-го рода через двойной интеграл.

Тогда поверхность S можно рассматривать как график функции , определенной на , или как график функции , определенной на , или как график функции , определенной на . Зафиксируем сторону поверхности, выбрав ту, которая является внешней, (нормаль образует острый угол с осью Z). Тогда

Рассмотрим теперь, например, третий интеграл. Так как это поверхностный интеграл 1-го рода от функции , то, переходя к двойному интегралу, получим

.

Но , поэтому

Аналогично получим

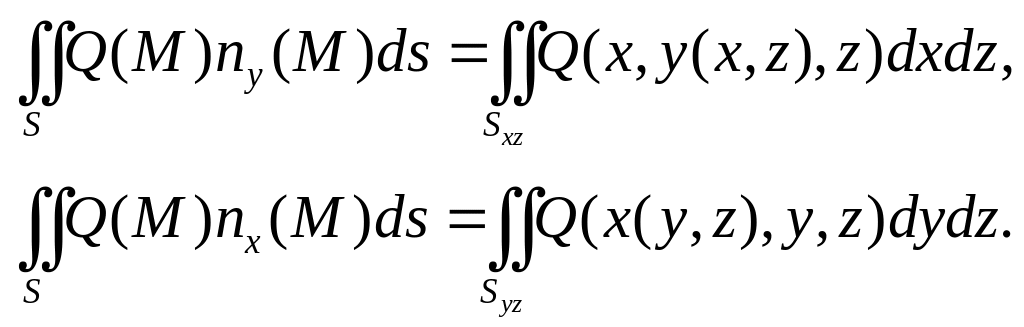
Тогда получаем, что

Это равенство позволяет вывести следующее "координатное" представление поверхностного интеграла 2-го рода

.

Пример 8.1. Вычислить поверхностный интеграл 2-го рода по треугольнику T, ограниченному плоскостями .

конец примера.

Вопрос 8.3. Стационарные скалярные и векторные поля.

Определение 8.2. Если каждой точке M некоторой области D поставлено в соответствие некоторое число u, то говорят, что на области D задано скалярное поле u.

Конец определения.

Определение 8.3. Скалярное поле называется стационарным, если оно явно не зависит от параметра t (t ‑ временная переменная) и нестационарным в противном случае.

Конец определения.

Таким образом, нестационарное скалярное поле имеет вид , а стационарное . Если на области D введена декартова система координат, то или .

Определение 8.4. Если каждой точке M некоторой области D поставлен в соответствие некоторый вектор , то говорят, что на области D задано векторное поле.

Конец определения.

Определение 8.5. Векторное поле называется стационарным, если оно явно не зависит от параметра t (t ‑ временная переменная) и нестационарным в противном случае. Стационарные векторные поля называются так же консервативными или динамическими.

Конец определения.

Таким образом, нестационарное векторное поле имеет вид , а стационарное . Если на области D введена декартова система координат, то векторное поле можно разложить по декартовому базису

или

.

Отсюда следует вывод, что задание векторного поля равносильно заданию трех скалярных полей P, Q и R. Эти скалярные поля будем называть компонентами или координатами векторного поля и обозначать иногда через и .