18. Ортогональность главных форм собственных колебаний.

Состоит в том, что работа внешних (внутренних сил) одной главной формы на перемещениях (деформациях) другой главной формы равна нулю. Докажем это, для чего рассмотрим две главные формы колебаний системы с частотами Ѡ_i и Ѡ_m_.(рис. 56) . Системы во время свободных колебаний будут иметь в качестве внешних сил инерционные силы масс, указанные на рис. 56.

Составим уравнение взаимности работ внешних сил:

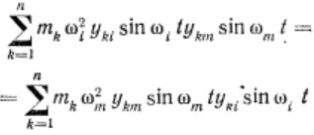
(3.79)

Или (3.80)

Т ак как Ѡ_i≠ Ѡ_m_,то равенство возможно лишь тогда, когда каждая часть (3.79) равна нулю, т.е. когда

(3.81)

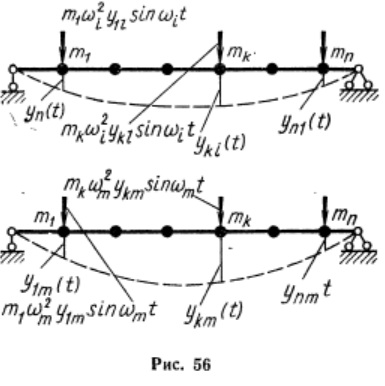
Последнее равенство выражает свойство ортогональности главных форм колебаний.

Свойство ортогональности главных форм колебаний, выраженное

1.Типы динамических воздействий, их характеристики и особенности.

Динамика сооружений - это специальный раздел строительной механики, посвященный методам расчета сооружений на динамические нагрузки.

Динамическими называются нагрузки, которые во время действия сообщают массам сооружения значительные ускорения, вызывая появление инерционных сил.

1. Неподвижная периодическая нагрузка характерна тем, что она многократно повторяется через определенные промежутки времени. Периодическая нагрузка может быть как непрерывной, так и прерывной.

Если непрерывная периодическая нагрузка изменяется по закону синуса или косинуса, то такая нагрузка называется вибрационной или гармонической. Создаются такие нагрузки различными механизмами, имеющими неуравновешенные массы вращающихся частей.

2.Кратковременная нагрузка характерна почти мгновенным действием, т.е. быстрым развитием и быстрым исчезновением (взрыв).

3. Ударная нагрузка характеризуется резким изменением скорости ударяемого тела. Ударную нагрузку создают падающие тела, всевозможные копры, молоты и т.д.

4.Подвижная нагрузка постоянного или переменного значения, меняющая свое положение на сооружении (поезда, автомобили, мостовые краны и т.д.).

5.Сейсмическая нагрузка - это беспорядочное движение почвы, толчки, удары и т.д. Динамический расчет сооружений состоит в определении внутренних усилий и

перемещений от динамических нагрузок, значение и характер действия которых известны, или в проверке системы на резонанс при периодически повторяющейся нагрузке определенной частоты.

6. Ветровая нагрузка

7. Дифференциальное уравнение колебаний без учета сил сопротивлений.

При Р=0

Из решения видно что свободн. колеб-я явл-ся гармоничными (по з-ну Sin, Cos) с частотой w.

w – круговая частота свободных колеб-й

16.Собственные колебания в системах с n-степенями свободы

П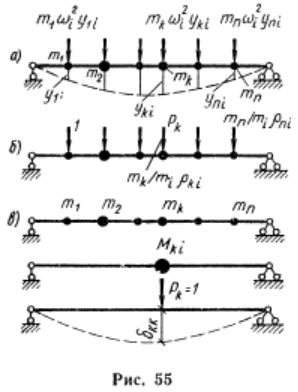 оложение масс при свободном движении системы определяет ее форму в любой момент времени. Поскольку свободное движение масс в системе с n степенями свободы является сложным, состоящим из n колебаний с n различными частотами ω_i, то форма движения системы в общем случае переменна-отношение перемещений отдельных масс непрерывно меняются. Однако всегда можно задать такие начальные условия движения системы, чтобы колебания всех масс происходили с одной какой-либо частотой ω_i из спектра частот. Такие колебания и соответствующие им формы называются главными или нормальными. Очевидно, что число главных форм колебаний равно числу степеней свободы системы. В главных формах колебаний отношения перемещений любых масс всегда постоянны и не зависят от времени. Следовательно, главные формы определяются перемещениями y₁_z(t)…y_nz(t) или их отношениями в любой момент времени.

Главную форму колебаний с частотой ω_iможно определить перемещениями масс от действующих на систему инерционных сил (рис.55а). Поделив их на силу инерции какой-либо, например первой, массы, получим схему сил, определяющую главную форму, в которой силы зависят не от самих перемещений, а от их отношений p_ki=y_ki:y₁_i(рис.55б). Отметим, что при равных массах отношение сил, определяющих главную форму, равно отношению перемещений под этими силами. Так, например, сила P_k(рис.55б) равна y_ki:y_1i.Покажем теперь, что перемещение любой массы в главной форме или всех масс вместе можно определять, как перемещение некоторой воображаемой системы с одной степенью свободы. Дифференциальное уравнение колебаний массы m_k в главной форме с частотой ω_i:

По (3.76) легко определяется частота, если задана главная форма колебаний. Это выражение можно представить еще так:

Масса M_ki– это приведенная масса, соответствующая частоте ω_i, которую можно поместить на месте массы m_k,а остальные массы с балки снять, чтобы получить систему с одной степенью свободы.

9 . Определение характеристик колебательного движения. Частотный опредлелитель: