
- •Предмет теории вероятностей. Основные понятия теории вероятностей. Статистическое и классическое определение вероятности
- •Аксиомы тв
- •Размещения, перестановки и сочетания
- •Правила суммы и произведения
- •Условная вероятность
- •Формула полной вероятности. Формула Байеса
- •Дискретные случайные величины. Числовые характеристики дискретной случайной величины и их свойства
- •Функция распределения и её свойства
- •Непрерывные случайные величины. Плотность вероятности и её свойства. Числовые характеристики непрерывной случайной величины
- •Распределения дискретной случайной величины
- •Распределения непрерывной случайной величины
- •Закон больших чисел
- •Понятие о теореме Ляпунова. Центральная предельная теорема
- •Многомерные случайные величины. Определение системы случайных величин. Закон распределения вероятностей дискретной двумерной случайной величины
- •Функция распределения двумерной случайной величины и её свойства
- •Двумерная плотность вероятности и её свойства. Нахождение функции распределения системы по известной плотности распределения
- •Зависимые и независимые случайные величины. Корреляционый момент. Коэффициент корреляции
- •Коррелированность и зависимость случайных величин. Нормальный закон распределения на плоскости
- •Линейная регрессия. Прямые линии среднеквадратической регрессии. Линейная корреляция. Нормальная корреляция.
- •Основные понятия математической статистики. Числовые характеристика вариативного ряда
- •Основные понятия математической статистики. Числовые характеристика вариативного ряда
Понятие о теореме Ляпунова. Центральная предельная теорема
Теорема Ляпунова — теорема в теории вероятностей, устанавливающая некоторые общие достаточные условия для сходимости распределения сумм независимых случайных величин к нормальному закону.
Центральная предельная теорема. Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.
центральная предельная теорема устанавливает условия, при которых сумма большого числа независимых слагаемых имеет распределение, близкое к нормальному.
Пусть Х1, Х2, ..., Хn,,…- последовательность независимых случайных величин, каждая из которых имеет конечные математическое ожидание и дисперсию:
M(Xk)=ak,
D(Xk)=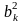 .
.
Sn = X1
+ X2+
. . . +Хn,An=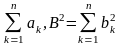 ,
,
Обозначим функцию распределения нормированной суммы через
Fn(x)=P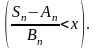
Говорят,
что к последовательности Х1,
Х2,
...
применима
центральная предельная теорема, если
при любом x
функция распределения нормированной
суммы при п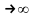 стремится
к нормальной функции распределения:
стремится
к нормальной функции распределения:
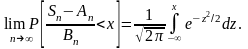
В
частности, если все случайные величины
X1,
Х2,...
одинаково распределены, то к этой
последовательности применима центральная
предельная теорема, если дисперсии всех
величин Xi(i=
1,
2,
...)
конечны и отличны от нуля. А.М. Ляпунов
доказал, что если для любого δ> 0 при
п
отношение
Ляпунова стремится
к нулю (условие
Ляпунова),
то
к последовательности Х1,
Х2,…
применима
центральная предельная теорема.Сущность
условия Ляпунова состоит в требовании,
чтобы каждое слагаемое суммы (Sn—
Ап)/Впоказывало
на сумму ничтожное влияние.
стремится
к нулю (условие
Ляпунова),
то
к последовательности Х1,
Х2,…
применима
центральная предельная теорема.Сущность
условия Ляпунова состоит в требовании,
чтобы каждое слагаемое суммы (Sn—
Ап)/Впоказывало
на сумму ничтожное влияние.
Многомерные случайные величины. Определение системы случайных величин. Закон распределения вероятностей дискретной двумерной случайной величины
Очень
часто результат испытания характеризуется
не одной СВ, а некоторой системой
случайных величин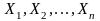 ,
которую называют также многомерной
(n-мерной) случайной величиной или
случайным вектором Х = (
),
т.е. n-мерная случайная величина –
упорядоченный набор nслучайных
величин
,
которую называют также многомерной
(n-мерной) случайной величиной или
случайным вектором Х = (
),
т.е. n-мерная случайная величина –
упорядоченный набор nслучайных
величин
Случайные величины , входящие в систему, могут быть как дискретными, так и непрерывными.
Двумерная сл.вел – упорядоченный набор 2-х случайных величин (X,Y),Где X. Y- компоненты(составляющие) 2-мерной сл.вел.
Закон распределения 2-мерной сл.вел – перечень возможных значений этой величины,т.е. упорядоченных пар(х,у) с указанием соответствующих им вероятностей(рис 5)
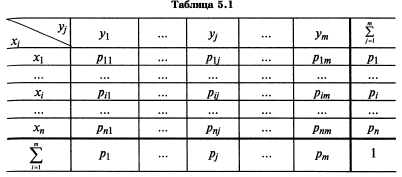
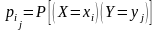 .
.
Так
как события
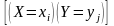 (i
= 1,2,...,n; j = 1,2,...,m),
состоящие в том, что СВ Х примет значение
(i
= 1,2,...,n; j = 1,2,...,m),
состоящие в том, что СВ Х примет значение
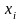 ,
а СВ Y
- значение
,
а СВ Y
- значение
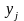 ,
несовместны и единственно возможны,
т.е. образуют полную группу, то сумма их
вероятностей (всех клеток таблицы )равна
единице, т.е.:
,
несовместны и единственно возможны,
т.е. образуют полную группу, то сумма их
вероятностей (всех клеток таблицы )равна
единице, т.е.:
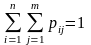
Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих. Т.к. События (x1,y1), (x1,y2) … (x1, ym) несовместны, то p(x1) по теореме сложения:
p(x1)= р(x1,y1)+р(x1,y2)+ …+р (x1, ym). Т.о. вероятность того, что Х примет значение х1 равна сумме вероятностей столбца «хi». Аналогично, чтобы найти вероятность yj нужно сложить вероятности соответствующей строки.
