6.Осевой момент инерции мт и системы мт. Теорема Штейнера.
Момент инерции — скалярная физическая величина, мера инертности тела во вращательном движении вокруг оси и = сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).Единица измерения СИ: кг·м². При поступат движении мера энертн – масса, а при вращательном-момент энерции.
Момент
импульса мт:
;
;
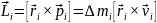Момент импульса тв.тела:
Oсевым
моментом инерции называется величина
,
равная сумме произведений элементарных
масс mi на квадраты их расстояний до
оси:
,
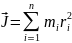где: mi — масса i-й точки, ri — расстояние
от i-й точки до оси.
a
Теорема Гюйгенса-Штейнера
Момент инерц тела ,относительно произвольно
выбранной
оси а = сумме моментов инерции тел
, относительно //-ой ей оси
,проходящей
ч/з центр масс тела, и произведению массы
тела m на квадрат расстоян м/д ними d:
7. Основное уравнение динамики вращательного движения
Пусть материальная точка массы m вращается
относительно оси ОО΄. Обозначим r - радиус-
вектор, проведенный от оси вращения до точки
приложения силы F.Моментом
силы F относительно оси вращения называется
вектор M, равный векторному произведению радиус-вектора на вектор силы M = [r·F] и направленный по оси вращения в сторону, определяемую по правилу правого буравчика. Модуль вектора момента силы равен M = F·r·sinα, где α - угол между векторами r и F.
Момент
инерции. Моментом инерции системы (тела)
относительно оси вращения называется
физическая величина, равная сумме
произведений масс n материальных точек
системы на квадраты их расстояний до
рассматриваемой оси:
. В случае непрерывного распределения
масс эта сумма сводится к интегралу
, где интегрирование производится по
всему объему тела.
Для
тела, которое вращается вокруг оси, 2
закон Ньютона формулируется следующим
образом: В инерциальной системе отсчёта
момент равнодействующей всех сил,
приложенных к телу, относительно оси
вращения равен произведению момента
инерции этого тела и сообщаемого ему
углового ускорения:I
– это выражение называется основным
уравнением динамики вращательного
движения.
8. Законы изменения и сохранения момента импульса
Моментом импульса тела называется физическая векторная величина, характеризующая его механическое состояние при вращательном движении и равная произведению момента инерции тела и его угловой скорости:
.
.
Скорость изменения момента импульса
со временем=суммарному моменту сил,
действующих на частицу.
.
,
.
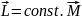=0.этот
закон наз. Законом изменения мом.импульса.
Закон сохранения момента импульса.
Из закона изменения момента импульса для системы тел вытекает закон сохранения момента импульса применительно к механике:
момент импульса системы тел сохраняется неизменным при любых взаимодействиях внутри системы, если результирующий момент внешних сил, действующих на нее, равен нулю. При использовании этого закона моменты импульса и сил необходимо брать относительно одно и той же оси.
Следствия из закон сохранения момента импульса:
· в случае изменения скорости вращения одной части системы другая также изменит скорость вращения, но в противоположную сторону таким образом, что момент импульса системы не изменится;
· если момент инерции замкнутой системы в процессе вращения изменяется, то изменяется и ее угловая скорость таким образом, что момент импульса системы останется тем же самым;
· в случае, когда сумма моментов внешних сил относительно некоторой оси равняется нулю, момент импульса системы относительно этой же оси остается постоянным.