27. Бинарное дерево. Способы прохождения дерева.
Бинарное дерево-это конечное множество элементов, которое либо пусто, либо содержит один элемент, а остальные элементы множества делятся на два непересекающихся подмножества, каждое из которых само является бинарным деревом. Эти подмножества называются левым и правым поддеревьями исходного дерева.
Глубина бинарного дерева - это максимальный уровень листа дерева, что равно длине самого длинного пути от корня к листу дерева.
Для дерева вводится понятие обхода – порядок просмотра элементов дерева.
Существует 6 способа обхода бинарного дерева.
КЛП – сверху вниз
ЛКП – слева направо
ПКЛ – справа налево
ЛПК – снизу вверх
ПЛК
КПЛ
28. Бинарное дерево поиска. Построение, использование.
Бинарное дерево поиска является нелинейной структурой для хранения множества элементов. Как и любая списковая структура, дерево должно допускать вставку, удаление и поиск элементов. Для поискового дерева требуется такая операция вставки, которая правильно располагает новый элемент. Рассмотрим, например, вставку узла 8 в дерево BinSTree_1. Начав с корневого узла 25, определяем, что узел 8 должен быть в левом поддереве узла 25 (8<25). В узле 10 определяем, что место узла 8 должно быть в левом поддереве узла 10, которое в данный момент пусто. Узел 8 вставляется в дерево в качестве левого сына узла 10.
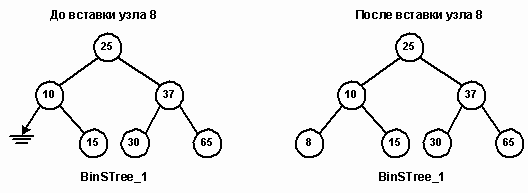
До каждого вставляемого в дерево узла существует конкретный путь. Тот же путь может использоваться для поиска элемента. Поисковый алгоритм берет ключ и ищет его в левом или в правом поддереве каждого узла, составляющего путь.
В связанном списке операция удаления отсоединяет узел и соединяет предшествующий ему узел с следующим узлом. На бинарном дереве поиска подобная операция намного сложнее, так как узел может нарушить упорядочение элементов дерева. Рассмотрим задачу удаления корня из BinSTree_1. В результате появляются два разобщенных поддерева, которым требуется новый корень.
Класс BinSTree – это класс, реализующий функциональность бинарного поискового дерева. Он содержит деструктор, конструктор копирования и перегруженные операторы присваивания, позволяющие инициализировать объекты и играющие роль операторов присваивания. Деструктор отвечает за очистку списка. Он и операторы присваивания вместе с методом ClearList вызывают скрытый метод DeleteTree. Мы также включили сюда скрытый метод CopyTree для использования в конструкторе копирования и перегруженном операторе "=".
Использование бинарных деревьев поиска Создание примеров деревьев поиска.
Функция MakeCharTree использовалась для создания ряда бинарных деревьев с символьными данными.
Симметричный метод прохождения.
При симметричном прохождении бинарного дерева сначала посещается левое поддерево узла, затем - сам узел и наконец правое поддерево. Когда этот метод прохождения применяется к бинарному дереву поиска, узлы посещаются в сортированном порядке. Симметричное прохождение бинарного дерева гарантирует, что для каждого узла меньшие узлы находятся в левом поддереве, а большие – в правом. В результате узлы проходятся в порядке возрастания.