
10. Постулаты квантовой механики.
Как известно, в
классической механике состояние частицы
определяется заданием её координаты и
импульса. Зная эти величины в нач. момент
времени и используя второй закон Ньютона,
можно определить состояние частицы в
любой момент времени. Для микрочастиц,
поскольку они обладают волновыми
св-вами, точное задание их координат и
импульса в один и тот же момент времени
невозможен
для описания движения микрочастиц
нельзя использовать II
закон Ньютона и тем самым методы
классической механики. Поэтому в начале
20-х годов прошлого столетия для описания
поведения микрочастиц была построена
новая послед.теория, в основе которой
лежат постулаты, отличающиеся коренным
образом от постулатов, лежащих в основе
классической механики. Эта новая теория
получила название квантовой механики.
В рамках данной теории удалось описать
как корпускулярные, так и волновые св-ва
микрочастиц. Следует сказать, что
квантовая механика по своей сути является
вероятностной теорией, т.е. происходящие
в микромире события можно предсказать
только с некоторой вероятностью → в
квантовой механике главная задача
состоит не в точном предсказании событий,
как это делается в классической механике,
а в определении вероятностей этих
событий. Зная вероятности этих событий
можно, зная правила, которые разработаны
в квантовой механике, найти средние
значения некоторых физических величин,
которые можно измерить экспериментально.
В основе квантовой механики лежат
след.постулаты: 1) Состояние частицы
задается волновой функцией
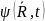 ,
которая является комплексной величиной.
2) Если какая-либо система способна
находиться в состоянии, описываемом
волновой функцией ψ1 и в другом
состоянии волновой функцией ψ2 ,
то она может находиться в состоянии,
описываемом функцией ψ=с1ψ1+с2ψ2
, где с1 и с2 –произвольные,
вообще говоря, комплексные числа. 3)
Каждой механической величине L
сопоставляется линейный самосопряженный
оператор L→
,
которая является комплексной величиной.
2) Если какая-либо система способна
находиться в состоянии, описываемом
волновой функцией ψ1 и в другом
состоянии волновой функцией ψ2 ,
то она может находиться в состоянии,
описываемом функцией ψ=с1ψ1+с2ψ2
, где с1 и с2 –произвольные,
вообще говоря, комплексные числа. 3)
Каждой механической величине L
сопоставляется линейный самосопряженный
оператор L→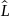 . 4) Среднее значение величины L
для системы, находящейся в состоянии,
которое описывается волновой функцией
ψ определяется формулой:
. 4) Среднее значение величины L
для системы, находящейся в состоянии,
которое описывается волновой функцией
ψ определяется формулой:
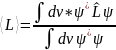 .
5) волновая функция ψ подчиняется
уравнению Шредингера:
.
5) волновая функция ψ подчиняется
уравнению Шредингера:
 ,
где
,
где
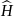 -оператор
Гамильтона(оператор полной энергии).
-оператор
Гамильтона(оператор полной энергии).
Поскольку волновая функция является комплексной величиной, то → её экспериментально определить невозможно. Физическую интерпретацию волновой функции дал Борн, согласно которому квадрат модуля волновой функции ψ представляет собой плотность вероятности нахождения частицы в момент времени t в точке, которая описывается радиус-вектором R.
P= 2=ψψ*
(1). Под плотностью вероятности понимается
вероятность нахождения частицы в единице
объёма. Из вышесказанного следует, что
вероятность нахождения частицы в объеме
dV в момент времени t
можно найти след.образом:
2=ψψ*
(1). Под плотностью вероятности понимается
вероятность нахождения частицы в единице
объёма. Из вышесказанного следует, что
вероятность нахождения частицы в объеме
dV в момент времени t
можно найти след.образом:
 (2). Как известно, полная вероятность
любого события равна 1, поэтому из (2)
→волновая функция должна удовлетворять
след. условию:
(2). Как известно, полная вероятность
любого события равна 1, поэтому из (2)
→волновая функция должна удовлетворять
след. условию:
 (3), где интеграл берется по всему
пространству. Условие (3) в квантовой
механике называется условием нормировки.
Это связано с тем, что при решении
уравнения Шредингера волновая функция
определяется с точностью до постоянного
множителя, который определяется из
условия(3). Отметим, что в квантовой
механике волновая функция является
основной величиной, т.к. зная её, можно
описать всё физические св-ва микрочастиц,
в частности поскольку волновая функция
удовлетворяет принципу суперпозиций,
то с ее помощью можно описать волновые
св-ва микрочастиц.
(3), где интеграл берется по всему
пространству. Условие (3) в квантовой
механике называется условием нормировки.
Это связано с тем, что при решении
уравнения Шредингера волновая функция
определяется с точностью до постоянного
множителя, который определяется из
условия(3). Отметим, что в квантовой
механике волновая функция является
основной величиной, т.к. зная её, можно
описать всё физические св-ва микрочастиц,
в частности поскольку волновая функция
удовлетворяет принципу суперпозиций,
то с ее помощью можно описать волновые
св-ва микрочастиц.
11.
Волновая функция и ее статистический
смысл
Волнова́я фу́нкция, или
пси-функция ![]() — комплекснозначная
функция, используемая в
квантовой
механике для описания
чистого
состояния системы. Является
коэффициентом разложения вектора
состояния по базису (обычно
координатному):
— комплекснозначная
функция, используемая в
квантовой
механике для описания
чистого
состояния системы. Является
коэффициентом разложения вектора
состояния по базису (обычно
координатному):
Физический смысл волновой функции заключается в том, что согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точке пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении.
Мы привыкли к тому, что физически реальное - измеримо. Бор и Гейзенберг сделали обратное высказывание: " Принципиально неизмеримое - физически нереально." Поэтому "не надо говорить о вещах, которые невозможно измерить" (Фейнман). Поскольку из соотношения неопределенностей следует, что частица не имеет одновременно импульс и координату, то не следует об этом и говорить. А "говорить" следует о волновой функции, которая описывает микросостояние системы, ее волновые свойства.
Де Бройль связал со свободно движущейся частицей плоскую волну. Известно [cм. (1.5), (1.6)], что плоская волна, распространяющаяся в направлении оси х описывается уравнением
S=Acos(t- kх+О)
или в экспоненциальной форме
S=АOехр[i(t- kх+О)].
Заменив в соответствии с (1) и (2) и k=2/ через Е и p, уравнение волны де Бройля для свободной частицы пишут в виде
=АOехр[(-i/![]() )(Еt-
pх)]. (16)
)(Еt-
pх)]. (16)
(в квантовой механике показатель экспоненты берут со знаком минус, но поскольку физический смысл имеет || 2, то это [cм.(16)] несущественно).
Функцию называют волновой функций или пси-функцией. Она, как правило, бывает комплексной.
Интепретацию волновой функции дал в 1926 г. Борн: квадрат модуля волновой функции определяет вероятность того , что частица будет обнаружена в пределах объема dV:
dP=|| 2 dV=*dV (17)
где * - комплексно - сопряженная волновая функция.
Величина || 2=* = dP/ dV - имеет смысл плотности вероятности.
Интеграл от (17), взятый по всему пространству, должен равняться единице (вероятность достоверного события Р=1).
![]() (18)
(18)
Выражение (18) называют условием нормировки.
Отметим еще раз, что волновая функция описывает микросостояние частицы, ее волновые свойства и она позволяет ответить на все вопросы, которые имеет смысл ставить. Например, найти энергию и импульс частицы. Для этого следует вычислить следующие частные производные по координате х и времени t:
![]()
откуда
![]() (19)
(19)
Для
волновых функций справедлив принцип
суперпозиции, заключающийся
в том, что если система может пребывать
в состояниях, описываемых волновыми
функциями
![]() и
и
![]() ,
то она может пребывать и в состоянии,
описываемом волновой функцией
,
то она может пребывать и в состоянии,
описываемом волновой функцией
![]() при
любых комплексных
при
любых комплексных
![]() и
и
![]() .
.
Очевидно,
что можно говорить и о суперпозиции
(сложении) любого числа квантовых
состояний, то есть о существовании
квантового состояния системы, которое
описывается волновой функцией
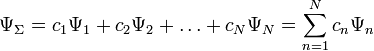 .
.
В
таком состоянии квадрат модуля
коэффициента
![]() определяет
вероятность того, что при измерении
система будет обнаружена в состоянии,
описываемом волновой функцией
определяет
вероятность того, что при измерении
система будет обнаружена в состоянии,
описываемом волновой функцией
![]() .
.
Поэтому
для нормированных волновых функций
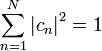 .
.
