2) Вычислить спектральную плотность амплитуды и спектр энергии прямоугольного сигнала

Рассмотрим прямоугольный сигнал с амплитудой А и длительностью . Его спектральная плотность энергии равна

(2.24)

Эта функция представлена на рис.2.10.

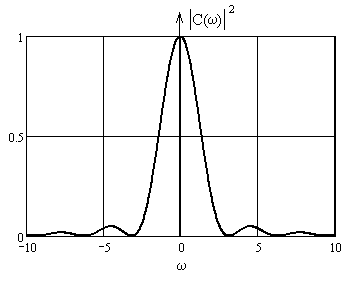
Рис.2.10

Этот спектр обладает минимумами и максимумами. Почему? Если рассмотреть асимптотику этого спектра по максимумам, то мы опять получим квадратичную асимптотику вида

Замена на Т/2

Билет 6

1) Отражение сигнала от земной поверхности и двулучевое распространение. Зависимость мощности принятого сигнала от расстояния. Дальность радиосвязи с учетом сигнала, отраженного от земли.

Сначала обратимся к изучению двулучевого распространения гармонического сигнала. Оно встречается тогда, когда передающая и приемная антенны подняты над землей и разнесены на достаточно большое расстояние. Соответствующая схема передачи сигнала изображена на рис. 2.1. Как видно из рисунка в точку приема попадают два сигнала двумя различными путями: прямой сигнал проходит расстояние R₀, а отраженный от земной поверхности сигнал - расстояние (R₁+R₂).

Рис. 2.1. Двулучевой канал связи

Сделаем следующие упрощающие предположения. Коэффициент отражения Френеля от земли будем считать равным –1. Это справедливо для волны любой поляризации, если угол падения  достаточно мал. Более подробные сведения о свойствах коэффициентов отражения Френеля от земной поверхности можно найти в учебниках по распространению радиоволн, например, в [42]. Будем полагать, что амплитуды прямого и отраженного сигналов равны, хотя в действительности амплитуда отраженного сигнала всегда немного меньше, во-первых, из-за того, что расстояние (R₁+R₂) больше расстояния R₀ и, во-вторых, из-за поглощения части энергии подающей волны в земле. Это предположение выполняется тем точнее, чем меньше угол . Единственное, что необходимо принять во внимание - это изменение фазы сигнала, отраженного от земли, по отношению к фазе прямого сигнала.

Таким образом, сумма прямого и отраженного сигналов может быть представлена в виде

, (2.1.9)

где =[(R₁+R₂)-R₀] – разность хода лучей.

Мощность принятого сигнала можно записать в виде

, (2.1.10)

где - мощность прямого сигнала на входе приемника.

Теперь определим величину разности хода  в зависимости от расстояния d и высот передающей и приемной антенн h_t и h_r. Из геометрии рис. 2.1 нетрудно определить, что

, . (2.1.11)

Преобразовав (2.1.11) и (2.1.12), получим следующие выражения

, . (2.1.12)

Мы предполагаем, что расстояние между передающей приемной антеннами большое, так что . Это позволяет упростить формулы (2.1.12) и получить следующие приближенные равенства

, . (2.1.13)

Вычитая (2.1.12) из (2.1.13), найдем, что разность хода равна

. (2.1.14)

Это дает возможность представить (2.1.10) следующим образом:

. (2.1.15)

Мощность прямого сигнала Р₀ зависит от параметров системы в соответствии с уравнением (2.1.5), которое получено для свободного пространства. Используя (2.1.5), выражение (2.1.15) преобразуем к виду

. (2.1.16)

Отсюда следует, что мощность принятого сигнала в случае двулучевой модели канала зависит от параметров системы и расстояния d между приемной и передающей антеннами сложным образом. В частности, имеется множитель

, (2.1.17)

который часто называют множителем ослабления земли. График функции g в зависимости от расстояния d показан на рис. 2.2 для λ=0.33 м (f=900 MГц), h_t=20 м, h_r=2 м.

Рис. 2.2. Множитель земли g(d)

В поведении функции g(d) можно выделить две области: область интерференции прямого и отраженного сигналов, где мощность принятого сигнала имеет периодический характер, и область регулярного затухания сигнала, где мощность сигнала непрерывно уменьшается с расстоянием. Граница между этими областями принимается на расстоянии, где наблюдается первый максимум функции g(d), если двигаться в направлении уменьшения дистанции d. Это условие выполняется, когда

. (2.1.18)

Отсюда находим, что граница между указанными областями определяется из выражения

. (2.1.19)

В данном примере, когда несущая частота f₀=900 MГц, расстояние d_гр=480 м. Если f₀ увеличить в два раза до 1800 MГц, то d_гр=960 м. Нетрудно заметить, что дальность d_гр зависит от частоты линейно.

Когда расстояние до приемника значительно больше расстояния d_гр, аргумент синуса становится много меньше единицы и справедливо приближенное равенство . В этой области множитель ослабления земли (2.1.17) можно записать в более простом виде

. (2.1.20)

Теперь можно упростить формулу (2.1.16). В результате, получим, что мощность на входе приемника равна

. (2.1.21)

Важный вывод, следующий из (2.1.21), заключается в том, что мощность принимаемого сигнала убывает с расстоянием обратно пропорционально четвертой степени . Это существенно более сильная зависимость ослабления сигнала по сравнению со случаем свободного пространства, где мощность принимаемого сигнала убывает с расстоянием обратно пропорционально второй степени. Поскольку мощность принимаемого сигнала пропорциональна квадрату амплитуды напряженности электрического поля в точке расположения приемной антенны, то напряженность поля убывает с расстоянием обратно пропорционально второй степени. Такая закономерность ослабления поля впервые была установлена академиком Введенским, и носит название квадратичной формулы Введенского.