
- •Билет 1
- •1) Спектральная плотность амплитуды и спектр энергии действительного сигнала. Их основные свойства.
- •2) Канальная модель Кларка и спектр Джейкса.
- •Билет 2
- •1) Три способа представления узкополосного сигнала. Принцип работы модулятора и демодулятора.
- •2) Вычислить спектральную плотность амплитуды и спектр энергии сигнала
- •Билет 3
- •1) Комплексная амплитуда узкополосного сигнала. Рассмотреть пример вычисления комплексных амплитуд сигналов для антенной решетки в случае приема плоской волны.
- •2) Вычислить спектральную плотность амплитуды и спектр энергии сигнала
- •Билет 4
- •1) Случайные узкополосные сигналы. Релеевское распределение амплитуды и замирания сигнала в многолучевом канале связи.
- •2) Вычислить спектральную плотность амплитуды и спектр энергии сигнала
- •Билет 5
- •1) Передача сигнала в свободном пространстве. Связь мощностей принятого и передаваемого сигналов. Дальность радиосвязи в свободном пространстве.
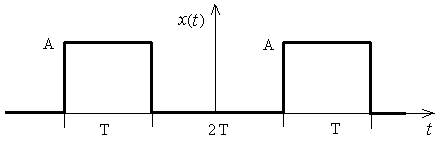
- •2) Вычислить спектральную плотность амплитуды и спектр энергии прямоугольного сигнала
- •1) Отражение сигнала от земной поверхности и двулучевое распространение. Зависимость мощности принятого сигнала от расстояния. Дальность радиосвязи с учетом сигнала, отраженного от земли.
- •2) Вычислить спектр сигнала в виде функции скачка (функции включения).
- •1) Плоский канал связи. Частотно-селективный канал связи.
- •2) Найти асимптотическое поведение спектра энергии треугольного сигнала вида при больших частотах, не вычисляя его спектр.
- •Билет 8
- •1) Функция автокорреляции действительного детерминированного сигнала. Взаимная функция корреляции двух действительных детерминированных сигналов.
- •2) Найти асимптотическое поведение спектра энергии сигнала вида
- •1) Случайные узкополосные сигналы. Релеевское и Райсовское распределение амплитуды.
- •2) Найти асимптотическое поведение спектра сигнала вида
- •1) Функция взаимной корреляции двух гармонических сигналов с одинаковыми частотами. Функция взаимной корреляции двух гармонических сигналов с кратными частотами.
- •2) Найти асимптотическое поведение спектра сигнала вида при больших частотах, не вычисляя его спектр.
- •1) Связь спектральных и корреляционных характеристик действительного сигнала.
- •2) Найти асимптотическое поведение спектра сигнала вида при больших частотах, не вычисляя его спектр.
- •1) Случайные сигналы и шумы. Функция плотности распределения. Нормальный случайный процесс. Одномерный и двумерный случаи.
- •2) Найти спектр сигнала вида . Найти спектр сигнала, который получается после интегрирования сигнала , используя свойство преобразования спектров при интегрировании сигналов.
- •Билет 13
- •1) Гармонический сигнал со случайной фазой. Найти одномерную функцию плотности распределения.
- •2) Вычислить спектральную плотность амплитуды и спектр энергии сигнала вида . Билет 14
- •1) Амплитудная модуляция, используемая в системах цифровой связи.
- •2) Найти функцию автокорреляции прямоугольного сигнала, длительность и амплитуда которого равны т и а соответственно.
- •Билет 15
- •1) Фазовая модуляция, используемая в системах цифровой связи.
- •2) Найти функцию автокорреляции гармонического сигнала .
- •1) Квадратурная амплитудная модуляция, используемая в системах цифровой связи.
- •2) Найти мощность гармонического сигнала .
- •1) Импульсная характеристика и передаточная функция многолучевого канала связи.
- •2) Гауссовская частотная манипуляция с минимальным частотным сдвигом, используемая в стандарте gsm.
- •1) Временная дисперсия в многолучевом канале связи, среднее значение и дисперсия задержки сигнала.
- •2) Каким образом преобразуется энергетический спектр сигнала при дифференцировании этого сигнала?
- •1) Частотная дисперсия в многолучевом канале связи, модель Кларка для многолучевого канала.
- •2) Каким образом преобразуется энергетический спектр сигнала при интегрировании этого сигнала?
- •1) Угловая дисперсия в многолучевом канале связи, Гауссова модель канала и ее сравнение с круговой моделью и моделью Кларка.
- •1) Оценка импульсной характеристики однолучевого канала связи.
- •2) Каким образом следует определять асимптотическое поведение спектра энергии сигнала при больших частотах, если а) сигнал имеет скачки; б) сигнал имеет скачки первой производной?
- •1) Пространственная корреляция сигналов.
- •2) Каким образом связаны между собой функция автокорреляции действительного сигнала и его спектр энергии ?
- •1) Оценка импульсной характеристики многолучевого канала при известной длине импульсной характеристики.
- •2) Какими свойствами обладают спектральная плотность амплитуды и спектр энергии , если сигнал является действительной функцией времени?
- •1) Оценка длины импульсной характеристики многолучевого канала связи.
- •2) Найти функцию автокорреляции сигнала вида
- •1) Оценка частотной передаточной функции многолучевого канала связи в ofdm системе связи.
2) Найти функцию автокорреляции сигнала вида
Билет 25
1) Оценка частотной передаточной функции многолучевого канала связи в ofdm системе связи.
Передача данных в такой системе связи осуществляется с помощью OFDM сигналов, причем каждый сигнал переносит информацию на ортогональных частотах, размещенных в пределах частотной полосы пропускания. Схематически, это изображено на рис. 8.13.

Рис. 8.13 Передача информации в системе с OFDM
Каждая клеточка на рисунке соответствует одному OFDM сигналу и одной поднесущей частоте. Для оценки канала передаются пилотные сигналы, для которых выделяются некоторые заданные позиции. Один пилотный сигнал показан на рис. 8.13. Строго говоря, для каждой позиции существует индивидуальный канальный коэффициент передачи, так как канал имеет вариации как по времени, так и по частоте. Однако параметры системы выбирают так, чтобы в соседних позициях отличие канальных коэффициентов было малым. Это дает возможность размещать пилотные сигналы достаточно редко в плоскости “частота-время” и использовать интерполяцию канальных оценок на те позиции, где передаются данные.
Рассмотрим линейный интерполяционный алгоритм. Предположим, что канальный коэффициент h является функцией времени t и частоты , и может быть приближенно представлен в виде
![]() , (8.4.1)
, (8.4.1)
где Δt=(t-t0) и Δν=(ν-ν0),
![]() - канальный коэффициент и его частные
производные в точке (t0, ν0),
соотвественно.
- канальный коэффициент и его частные
производные в точке (t0, ν0),
соотвественно.
Более удобно ввести следующие обозначения
![]() ,
,
![]() ,
,
![]() .
Тогда (8.4.1) можно переписать как.
.
Тогда (8.4.1) можно переписать как.
![]() . (8.4.2)
. (8.4.2)
Выражение (8.4.2) представляет собой уравнение плоскости. Оно имеет три параметра A, B и C, которые мы должны оценить, используя пилотные сигналы. Ясно, что одного пилотного сигнала для этого недостаточно, необходимо три или более пилотных сигналов.
Допустим, что имеется N пилотных
сигналов sj. Принятые
пилотные сигналы
![]() являются статистически независимыми.
Поэтому совместная плотность вероятности
равна произведению одномерных плотностей
вероятности и может быть записана в
виде
являются статистически независимыми.
Поэтому совместная плотность вероятности
равна произведению одномерных плотностей
вероятности и может быть записана в
виде
 . (8.4.3)
. (8.4.3)
Здесь принято во внимание, что
![]() и
и
![]() .
.
Подставим (8.4.2) в (8.4.3) и получим следующее выражение:
 . (8.4.4)
. (8.4.4)
Это выражение является функцией правдоподобия относительно параметров A, B и C. Максимально правдоподобные оценки этих параметров находятся из решения следующих трех уравнений.
 , (8.4.5)
, (8.4.5)
где коэффициенты
 (8.4.6)
(8.4.6)
Уравнения (8.4.5) и (8.4.6) справедливы для произвольного числа пилотных сигналов, произвольного их расположения и любого вида.
В качестве примера рассмотрим OFDM передачу с 4 пилотными сигналами, показанную на рис. 8.14.
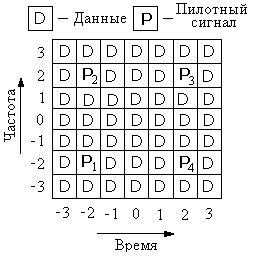
Рис. 8.14 OFDM передача с 4 пилотными сигналами.
Данные передаются на 45 позициях, в то
время как пилотные сигналы - на четырех
позициях в углах квадрата. Предполагается,
что пилотные сигналы имеют единичные
амплитуды. Расстояние между соседними
позициями принимается равным единице,
т.е.
![]() .
Точка с координатами (t0, ν0)
выбрана в начале координат (t0=0;
0=0).
.
Точка с координатами (t0, ν0)
выбрана в начале координат (t0=0;
0=0).
Из формулы (8.4.6) находим, что α12=α21=α13=α31=α23=α32=0. Благодаря симметричному расположению пилотных сигналов система уравнений (8.4.5) упрощается и может быть решена в явном виде. В результате мы получаем следующие оценки для параметров A, B и C:
![]() (8.4.7)
(8.4.7)
Поскольку оценка канального коэффициента
для пилотной позиции равна
![]() ,
уравнение (8.4.7) перепишем в другом виде.
,
уравнение (8.4.7) перепишем в другом виде.
![]() .
(8.4.8)
.
(8.4.8)
Канальные оценки для всех позиций, представленных на рис. 8.14, с учетом интерполяции вычисляются по формуле
![]() , (8.4.9)
, (8.4.9)
где индексы k и n показывают на рис. 8.14 номера позиций по времени и частоте.
Оценки (8.4.8) имеют ясный смысл. Оценка
![]() дает канальную оценку для точки начала
координат (k=0, n=0), а оценки
дает канальную оценку для точки начала
координат (k=0, n=0), а оценки
![]() - два градиента канальных коэффициентов
вдоль осей времени и частоты.
- два градиента канальных коэффициентов
вдоль осей времени и частоты.
Если канал не имеет вариаций («плоский» канал), то формула (8.4.9) упрощается и принимает вид
![]() . (8.4.10)
. (8.4.10)
Смысл такой оценки понятен. Для всех позиций принимается одна и та же оценка, равная среднему арифметическому между оценками канальных коэффициентов на пилотных позициях. Дисперсия оценки получается в 4 раза меньше, чем дисперсия одной пилотной оценки. Если принять ОСШ =1, дисперсия одной пилотной оценки равна средней мощности шума, которая принята равной единице. В таком случае оценка (8.4.10.) будет иметь дисперсию 0.25. Канальную оценку (8.4.10.) в литературе на английском языке иногда называют “block averaging”, что означает “усреднение блоком”.
Для оценки (8.4.9) также можно вычислить дисперсию. В этом случае дисперсия оценки зависит от индексов (k,n), т.е. от номера позиции в плоскости “частота-время”. Если принять ОСШ =1, то дисперсия оценки (8.4.9) равна
![]() . (8.4.11)
. (8.4.11)
Вычисленные по этой формуле значения дисперсии оценки приведены на рис. 8.15. Видно, что шумовая ошибка канального оценивания имеет наименьшее значение в центре квадрата, образованного пилотными сигналами, а наибольшее значение ошибки наблюдается в углах за пределами этого квадрата.
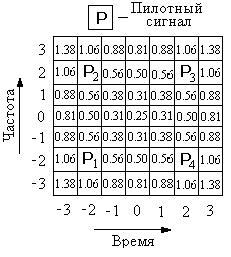
Рис.8.15 Дисперсии канальных оценок для различных позиций
Интерполяционные формулы (8.4.8), (8.4.9) и (8.4.11) легко обобщить на случай 4 пилотных сигналов с произвольной прямоугольной конфигурацией размещения. Такая конфигурация пилотных сигналов и необходимые обозначения представлены на рис. 8.16.

Рис. 8.16 Конфигурация пилотных сигналов в виде прямоугольника.
В этом случае оценки параметров A,
B и C и канальные оценки
![]() вычисляются по следующим формулам:
вычисляются по следующим формулам:
![]() , (8.4.12)
, (8.4.12)
![]() . (8.4.13)
. (8.4.13)
Дисперсия канальных оценок из-за шума при ОСШ =1 равна
![]() . (8.4.14)
. (8.4.14)
В системах с разнесенной передачей или в MIMO-системах на передающей стороне используется несколько антенн. В этом случае оценка канальных коэффициентов должна выполняться для каждой передающей антенны отдельно. Рассмотрим систему с двумя передающими и одной приемной антенной и предположим, что мощность передатчика делится между антеннами пополам. Тогда сигнал, принятый в одной позиции будет равен
![]() , (8.4.15)
, (8.4.15)
где h1 и h2 обозначают канальные коэффициенты, s1 и s2 представляют пилотные сигналы, а z есть шум приемника. Величина дает ОСШ, которое было бы, если бы на передающей стороне использовалась одна антенна и вся мощность передатчика излучалась через нее.
Оценить два канальных коэффициента из одного уравнения (8.4.15) невозможно. Мы должны использовать две или более позиций. Допустим, что две позиции используются для оценки канала, и принятые сигналы в этих позициях представим следующим образом:
![]() . (8.4.16)
. (8.4.16)
Здесь мы предполагаем, что обе позиции на плоскости “частота-время” выбраны рядом, так что канальные коэффициенты для обеих позиций равны между собой для каждой из двух антенн.
Выражение (8.4.16) удобно записать для анализа в матричной форме в виде
![]() , (8.4.17)
, (8.4.17)
где введены следующие обозначения
![]() . (8.4.18)
. (8.4.18)
Назовем матрицу S блоком пилотных
сигналов. Рассмотрим следующие два
блока пилотных сигналов
![]() и
и
![]() .
В первом случае каждая передающая
антенна использует только одну позицию
для оценки канала. Учитывая, что мощность,
передаваемая через одну антенну,
уменьшена вдвое, точность канального
оценивания уменьшится в два раза по
сравнению со случаем, когда имеется
одна передающая антенна. Во втором
случае каждая передающая антенна
использует обе позиции для оценки
канала. При этом блок пилотных сигналов
выбран так, что столбцы матрицы S2
являются взаимно ортогональными. Это
дает возможность сделать независимые
оценки каналов для обеих передающих
антенн. Действительно, система уравнений
(8.4.16) принимает вид
.
В первом случае каждая передающая
антенна использует только одну позицию
для оценки канала. Учитывая, что мощность,
передаваемая через одну антенну,
уменьшена вдвое, точность канального
оценивания уменьшится в два раза по
сравнению со случаем, когда имеется
одна передающая антенна. Во втором
случае каждая передающая антенна
использует обе позиции для оценки
канала. При этом блок пилотных сигналов
выбран так, что столбцы матрицы S2
являются взаимно ортогональными. Это
дает возможность сделать независимые
оценки каналов для обеих передающих
антенн. Действительно, система уравнений
(8.4.16) принимает вид
![]() . (8.4.19)
. (8.4.19)
Отсюда легко находим оценки канала
![]() . (8.4.20)
. (8.4.20)
Отсюда нетрудно найти, что точность канального оценивания для каждой антенны будет такой же, как при использовании одной передающей антенны. Этот результат понятен. Несмотря на уменьшение мощности, передаваемой через одну антенну, средняя мощность на одну пилотную позицию сохраняется одинаковой, так как две позиции используются каждой передающей антенной.
Чтобы увеличить точность канального оценивания, необходимо увеличить число пилотных позиций. Например, в случае трех или четырех позиций можно рекомендовать следующие блоки пилотных сигналов:
 ,
,  . (8.4.21)
. (8.4.21)
Столбцы каждой из этих матриц являются взаимно ортогональными, что позволяет делать канальное оценивание независимо для каждой передающей антенны. Уравнение (8.4.17) остается справедливым и в этих случаях. Поэтому легко найти канальные оценки в виде
![]() , (8.4.22)
, (8.4.22)
![]() . (8.4.23)
. (8.4.23)
Точность оценивания увеличивается в 1.5 и 2 раза в первом и втором случаях, соответственно.
Учтем теперь, что для каждой передающей антенны необходимо выполнить интерполяцию канальных оценок. Конфигурация пилотных позиций, которая позволяет выполнить и независимое канальное оценивание, и интерполяцию оценок, представлена на рис. 8.17. Видно, что имеется 16 пилотных позиций, разбитых на 4 группы. Внутри одной группы каждая передающая антенна использует свою последовательность сигналов, записанную в столбце блока пилотных сигналов. Канальную оценку, полученную с помощью последовательности сигналов, следует отнести к центру группы. Интерполяция канальных оценок выполняется с помощью уравнений (8.4.12), (8.4.13) и (8.4.14), где T и F имеют смысл интервалов между центрами групп по времени и частоте, как показано на рис. 8.17. Заметим, что параметры T и F в случае одной передающей антенны вычисляются несколько иначе, как показано на рис. 8.16.
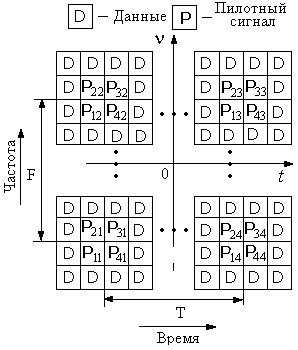
Рис. 8.17
Эту конфигурацию можно использовать также в случае трех или четырех передающих антенн. Для этого блок пилотных сигналов необходимо дополнить одним или двумя столбцами. Например, в случае четырех передающих антенн блок пилотных сигналов можно представить в виде

2) На входе антенной решетки имеется сигнал и собственный шум. Известен вектор комплексных амплитуд S сигнала, корреляционная матрица собственного шума равна единичной матрице. Найти весовой вектор, который обеспечивает максимальное ОСШ на выходе антенной решетки. Чему равно максимальное ОСШ?
